Puzzles
Parabola
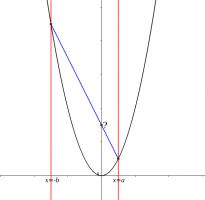
On a graph of \(y=x^2\), two lines are drawn at \(x=a\) and \(x=-b\) (for \(a,b>0\). The points where these lines intersect the parabola are connected.
What is the y-coordinate of the point where this line intersects the y-axis?
Show answer & extension
Hide answer & extension
The co-ordinates of the points where the lines intersect the parabola are \((a,a^2)\) and \((-b,b^2)\). Hence the gradient of the line between them is:
$$\frac{a^2-b^2}{a-(-b)}=\frac{(a+b)(a-b)}{a+b}=a-b$$
Therefore the y-coordinate is:
$$b^2 + b(a-b) = ba$$
Ferdinand Möbius, who discovered this property called the curve a Multiplicationsmaschine or 'multiplication machine' as it could be used to perform multiplication.
Extension
How could you use the graph of \(y=x^2\) to divide 100 by 7?
Two lines
Let A and B be two straight lines such that the gradient of A is the y-intercept of B and the y-intercept of A is the gradient of B (the gradient and y-intercept of A are not the same). What are the co-ordinates of the point where the lines meet?
Show answer & extension
Hide answer & extension
Let A have the equation \(y = mx + c\). B will have the equation \(y = cx + m\).
Therefore, \(mx + c = cx + m\).
Which rearranges to \(x(m - c) = m - c.\)
So \(x = 1\).
Substituting back in, we find \(y=m+c\).
The co-ordinates of the point of intersection are \((1,m+c)\).
Extension
Let \(a\), \(b\) and \(c\) be three distinct numbers. What can you say about the points of intersection of the parabolas:
$$y = ax^2 + bx + c\mathrm{,}\\
y = bx^2 + cx + a\mathrm{,}\\
\mathrm{and\ }y = cx^2 + ax + b$$
![](javascript:showlimage("parabola.png"))