Puzzles
Combining multiples
In each of these questions, positive integers should be taken to include 0.
1. What is the largest number that cannot be written in the form \(3a+5b\), where \(a\) and \(b\) are positive integers?
2. What is the largest number that cannot be written in the form \(3a+7b\), where \(a\) and \(b\) are positive integers?
3. What is the largest number that cannot be written in the form \(10a+11b\), where \(a\) and \(b\) are positive integers?
4. Given \(n\) and \(m\), what is the largest number that cannot be written in the form \(na+mb\), where \(a\) and \(b\) are positive integers?
Show answer & extension
Hide answer & extension
1. 7
2. 11
3. 90
First, if \(n\) and \(m\) share a common factor other than 1, there will be no largest number: any number that is not a multiple of the common factor will be impossible to make.
If \(n\) and \(m\) are coprime, then considered the remainders when the multiples of \(n\) are divided by \(m\). For example, if \(n=3\) and \(m=7\):
| Multiple | Remainder |
| 0 | 0 |
| 3 | 3 |
| 6 | 6 |
| 9 | 2 |
| 12 | 5 |
| 15 | 1 |
| 18 | 4 |
| 21 | 0 |
Once a number with a given remainder is reached, then all other numbers with that remainder can be reached by repeatedly adding \(m\). Once \(mn\) is reached, the remainders column will repeat itself. Before \(mn\), all remainders will appear (this can be shown by showing that there are \(m\) rows which much all have different remainders). Hence above \(mn\) all numbers can be made.
In the 3,7 example, the last remainder to be hit is 4. The highest number that cannot be made will be the highest number with remainder 4 that is less than 18 (when remainder 4 is hit).
In general, the last remainder will be hit at \(mn-n\). The number before this with the same remainder will be \(mn-n-m\). This will be the highest number that cannot be made.
Extension
Given \(n\), \(m\) and \(k\), what is the largest number that cannot be written in the form \(na+mb+kc\), where \(a\), \(b\) and \(c\) are positive integers?
Subsum
1) In a set of three integers, will there always be two integers whose sum is even?
2) How many integers must there be in a set so that there will always be three integers in the set whose sum is a multiple of 3?
3) How many integers must there be in a set so that there will always be four integers in the set whose sum is even?
4) How many integers must there be in a set so that there will always be three integers in the set whose sum is even?
Show answer & extension
Hide answer & extension
1) Yes, there must be either at least two even integers or at least two odd integers. The sum of two even integers is even. The sum of two odd integers is even.
2) Five.
3) Five.
4) An infinite number: in a list of odd integers, there will never be three integers which add up to an even number.
This puzzle leads naturally into the following extension:
Extension
How many integers must there be in a set so that there will always be \(a\) integers in the set whose sum is a multiple of \(b\)?
For which values of \(a\) and \(b\) will the answer to this be finite?
8 December
What is the largest number of factors which a number less than a million has?
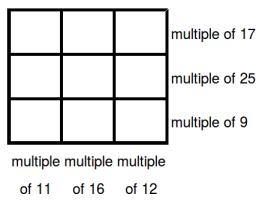
Fill in the digits
Can you place the digits 1 to 9 in the boxes so that the three digit numbers formed in the top, middle and bottom rows are multiples of 17, 25 and 9 (respectively); and the three digit numbers in the left, middle and right columns are multiples of 11, 16 and 12 (respectively)?
N
Consider three-digit integers \(N\) such that:
(a) \(N\) is not exactly divisible by 2, 3 or 5.
(b) No digit of \(N\) is exactly divisible by 2, 3 or 5.
How many such integers \(N\) are there?
Show answer & extension
Hide answer & extension
(b) implies that the digits of \(N\) are all 1 or 7, so \(N\) can only be 111, 117, 171, 177, 711, 717, 771 or 777. These are all divisible by 3, so no such integers \(N\) exist.
Extension
Consider 21-digit integers \(N\) such that:
(a) \(N\) is not exactly divisible by 2, 3 or 5.
(b) No digit of \(N\) is exactly divisible by 2, 3 or 5.
How many such integers \(N\) are there?