Puzzles
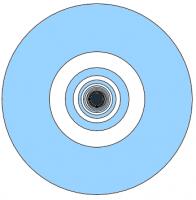
Dartboard
Concentric circles with radii 1, \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), ... are drawn. Alternate donut-shaped regions are shaded.
What is the total shaded area?
Show answer & extension
Hide answer & extension
The shaded area is:
$$\pi (1)^2 - \pi (\frac{1}{2})^2 + \pi (\frac{1}{3})^2 - \pi (\frac{1}{4})^2 + \pi (\frac{1}{5})^2 - ...$$
$$=\sum_{i=1}^\infty \frac{\pi (-1)^{i-1}}{i^2}$$
$$=\pi\sum_{i=1}^\infty \frac{(-1)^{i-1}}{i^2}$$
$$=\pi\left(\frac{\pi^2}{12}\right)$$
$$=\frac{\pi^3}{12}$$
Extension
Prove that
$$=\sum_{i=1}^\infty \frac{(-1)^{i-1}}{i^2}=\frac{\pi^2}{12}$$
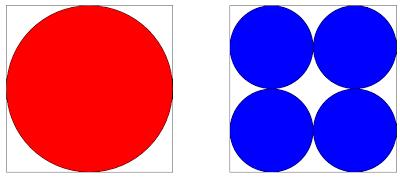
Circles
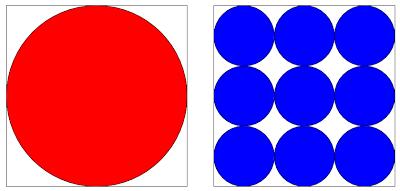
Which is largest, the red or the blue area?
Show answer & extension
Hide answer & extension
Let \(4x\) be the side length of the square. This means that the radius of the red circle is \(2x\) and the radius of a blue circle is \(x\). Therefore the area of the red circle is \(4\pi x^2\).
The area of one of the blue squares is \(\pi x^2\) so the blue area is \(4\pi x^2\). Therefore the two areas are the same.
Extension
Is the red or blue area larger?
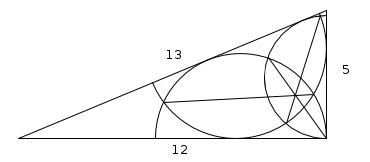
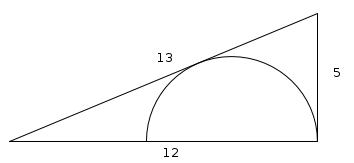
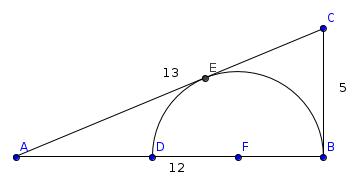
Semi circle in a triangle
This right-angled triangle above has sides of lengths 12cm, 5cm and 13cm. The diameter of the semicircle lies on the 12cm side and the 13cm side is a tangent to the circle. What is the radius of the semi circle?
Show answer & extension
Hide answer & extension
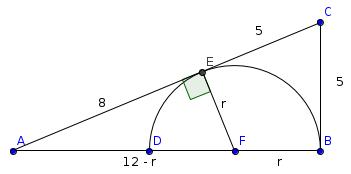
Label the triangle as follows:
EC and BC are both tangents to the circle so FEA is a right angle and the lengths EC and BC are equal, so the length of EC is 5. Let r be the radius of the circle.
Using Pythagoras' Theorem in triangle FEA:
$$8^2+r^2=(12-r)^2$$
$$64+r^2=144-24r+r^2$$
$$24r=80$$
$$r=\frac{80}{24}=\frac{10}{3}$$
Extension
What is the radius of the circle whose diameter lies on the 5cm side and to which the 12cm and 13cm sides are tangents?
What is the radius of the circle whose diameter lies on the 13cm side and to which the 12cm and 5cm sides are tangents?
Additional observation
For each pair of semi circles, draw a straight line between the two points where the semi circles intersect. These lines all meet at a point.
![](javascript:showlimage("dartboard.png"))
![](javascript:showlimage("circles.png"))
![](javascript:showlimage("circles-ext.png"))
![](javascript:showlimage("circle-and-triangle.png"))
![](javascript:showlimage("labelled-tricirc.png"))
![](javascript:showlimage("labelled-tricirc2.png"))
![](javascript:showlimage("ext1.png"))
![](javascript:showlimage("ext2.png"))
![](javascript:showlimage("ext3.png"))