Puzzles
15 December
If the numbers 1 to 7 are arranged 7,1,2,6,3,4,5 then each number is either larger than or a factor of the number before it.
How many ways can the numbers 1 to 7 be arranged to that each number is either larger than or a factor of the number before it?
14 December
What is the only palindromic three digit prime number which is also palindromic when written in binary?
13 December
Put the digits 1 to 9 (using each digit once) in the boxes so that the three digit numbers formed (reading left to right and top to bottom) have the desired properties written by their rows and columns.
The row marked sum is equal to the sum of the other two rows. The column marked sum is equal to the sum of the other two columns.
| odd | |||
| all digits even | |||
| sum | |||
| even | odd | sum |
Today's number is the largest three digit number in this grid.
12 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
| + | - | = -2 | |||
| - | - | - | |||
| + | ÷ | = 4 | |||
| + | ÷ | × | |||
| + | × | = 50 | |||
| = 4 | = -4 | = 10 |
The answer is the product of the digits in the red boxes.
11 December
This year, I was involved in starting Chalkdust Magazine. One of my roles for the magazine has been writing the £100 crossnumber puzzle.
What is the answer to 35 across in the first issue's crossnumber?
35A. The smallest number which is one more than triple its reverse. (3)
10 December
This number is divisible by 2. One more than this number is divisible by 3. Two more than this number is divisible by 5. Three more than this number is divisible by 7. Four more than this number is divisible by 11. Five more than this number is divisible by 13.
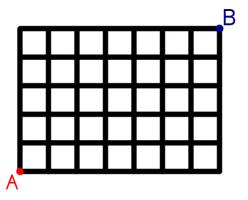
9 December
You start at A and are allowed to move either to the right or upwards.
How many different routes are there to get from A to B?
8 December
What is the largest number of factors which a number less than a million has?