Puzzles
Subsum
1) In a set of three integers, will there always be two integers whose sum is even?
2) How many integers must there be in a set so that there will always be three integers in the set whose sum is a multiple of 3?
3) How many integers must there be in a set so that there will always be four integers in the set whose sum is even?
4) How many integers must there be in a set so that there will always be three integers in the set whose sum is even?
Show answer & extension
Hide answer & extension
1) Yes, there must be either at least two even integers or at least two odd integers. The sum of two even integers is even. The sum of two odd integers is even.
2) Five.
3) Five.
4) An infinite number: in a list of odd integers, there will never be three integers which add up to an even number.
This puzzle leads naturally into the following extension:
Extension
How many integers must there be in a set so that there will always be \(a\) integers in the set whose sum is a multiple of \(b\)?
For which values of \(a\) and \(b\) will the answer to this be finite?
More doubling cribbage
Brendan and Adam are playing lots more games of
high stakes cribbage: whoever
loses each game must double the other players money. For example, if Brendan has £3 and Adam has £4 then Brendan wins, they will have £6
and £1 respectively.
In each game, the player who has the least money wins.
Brendan and Adam notice that for some amounts of
starting money, the games end with one player having all the money; but for other amounts, the games continue forever.
For which
amounts of starting money will the games end with one player having all the money?
Show answer & extension
Hide answer & extension
If Adam has £\(a\) and Brendan has £\(b\), we will write this as £\(a\):£\(b\).
First, we can take
\(a\) and \(b\) to have no common factors, as dividing both by a common factor gives an equivalent starting point. For example,
£3:£6 and £6:£12 will have exactly the same behaviour (imagine £6 and 3 £2 coins).
£\(a\):£\(b\) is also clearly equivalent to £\(b\):£\(a\) (but with the two players swapping places).
A game starting £\(a\):£\(b\) will end with one player having the money if \(a+b\) is a power of two. This is because:
If \(a+b=2^n\), then if \(n=1\), either the game has already ended or it sits at £1:£1 and is about to end. If \(n>2\), then the starting
position can be written as £\(2^n-k\):£\(k\) with \(k<2^n-k\). After another game this will be £\(2^n-2k\):£\(2k\). This is equivalent to
£\(2^{n-1}-k\):£\(k\). Therefore by
induction, if \(a+b=2^n\) then the
game ends with one player having all the money.
It can also be shown by induction, that if a game ends then it must be £\(a\):£\(b\)
with \(a+b=2^n\).
Extension
What would happen if the losing player has to triple the winning player's money?
Doubling cribbage
Brendan and Adam are playing high stakes cribbage: whoever loses each game must double the other players money. For example, if Brendan has £3 and Adam has £4 then Brendan wins, they will have £6 and £1 respectively.
Adam wins the first game then loses the second game. They then notice that they each have £180. How much did each player start with?
Show answer & extension
Hide answer & extension
Working backwards: before the second game, Brendan must have had £90 and so Adam had £270.
Before the first game, Adam must have had £135, so Brendan had £225.
Extension
After the next game, one player will have all the money and no more games can be played. Hence £135 and £225 lead to a finite number of games being played.
If the player with the most money always loses, which starting values £\(A\) and £\(B\) will lead to finite and infinite numbers of games?
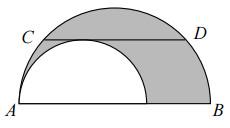
Two semicircles
The diagram shows two semicircles.
\(CD\) is a chord of the larger circle and is parallel to \(AB\). The length of \(CD\) is 8m. What is the area of the shaded region (in terms of \(\pi\))?
Show answer & extension
Hide answer & extension
The question does not fix the length of \(AB\), yet implies that there is a unique answer. Therefore we can take \(AB\) to be any length we like and expect the right answer. If \(AB\) is 8m long, then the unshaded semicircle has no area. Therefore the shaded area is \(\tfrac12\pi\times4^2=8\pi\)m.
Extension
How would you calculate the area if you don't assume that the length of \(AB\) doesn't affect the area?
What is the sum?
What is \(\displaystyle\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{15}+\sqrt{16}}\)?
Show answer
Hide answer
Start by rationalising the denominators:
$$\begin{array}{rl}
\frac{1}{\sqrt{n}+\sqrt{n+1}}
&=\frac{1}{\sqrt{n}+\sqrt{n+1}}\times\frac{\sqrt{n}-\sqrt{n+1}}{\sqrt{n}-\sqrt{n+1}}\\
&=\frac{\sqrt{n}-\sqrt{n+1}}{n-(n+1)}\\
&=\sqrt{n+1}-\sqrt{n}\end{array}$$
Therefore:
$$\begin{array}{rl}
\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{15}+\sqrt{16}}
&=(\sqrt{2}-\sqrt{1})+(\sqrt{3}-\sqrt{2})+\\&...+(\sqrt{15}-\sqrt{14})+(\sqrt{16}-\sqrt{15})\\
&=-\sqrt{1}+\sqrt{16}\\
&=3
\end{array}
$$
Between quadratics
\(p(x)\) is a quadratic polynomial with real coefficients. For all real numbers \(x\),
$$x^2-2x+2\leq p(x)\leq 2x^2-4x+3$$
\(p(11)=181\). Find \(p(16)\).
Show answer
Hide answer
$$x^2-2x+2=(x-1)^2+1$$
$$2x^2-4x+3=2(x-1)^2+1$$
Therefore the minimum point of both of these quadratics is \((1,1)\). \(p(x)\) will only be between these if:
$$p(x)=a(x-1)^2+1\quad\text{where }1\leq a\leq 2$$
We know that \(p(11)=181\), so:
$$\begin{array}{rl}
181&=p(11)\\
&=a(11-1)^2+1\\
&=100a+1
\end{array}$$
Therefore \(a=1.8\). This means that:
$$\begin{array}{rl}
p(16)&=1.8(16-1)^2+1\\
&=1.8\times225+1\\
&=406
\end{array}$$
24 December
Today's number is the largest possible remainder which can be obtained when dividing one of
the answers in this advent calendar by another answer smaller than it (not
including today's answer!).
23 December
This number is a prime number. If you treble it and add 16, the result is also prime. Repeating this will give 11 prime numbers in total (including the number itself).