Puzzles
Largest odd factors
Pick a number. Call it \(n\). Write down all the numbers from \(n+1\) to \(2n\) (inclusive). For example, if you picked 7, you would write:
$$8,9,10,11,12,13,14$$
Below each number, write down its largest odd factor. Add these factors up. What is the result? Why?
Show answer
Hide answer
Incredibly, the result will always be \(n^2\).
To see why, imagine writing every number, \(n+1\leq k\leq 2n\), in the form $$k=2^ab$$ where \(b\) is an odd number and also the \(k\)'s largest odd factor. The next largest number whose largest odd factor is \(b\) will be \(2^{a+1}b=2k\). But this will be larger than \(2n\), so outside the range. Therefore each number in the range has a different largest odd factor.
Each of the largest odd factors must be one of \(1, 3, 5, ..., 2n-1\), as they cannot be larger than \(2n\). But there are \(n\) odd numbers here and \(n\) numbers in the range, so each number \(1, 3, 5, ..., 2n-1\) is the highest odd factor of one of the numbers (as the highest odd factors are all different).
Therefore, the sum of the odd factors is the sum of the first \(n\) odd numbers, which is \(n^2\).
Square factorials
Multiply together the first 100 factorials:
$$1!\times2!\times3!\times...\times100!$$
Find a number, \(n\), such that dividing this product by \(n!\) produces a square number.
Show answer & extension
Hide answer & extension
First, look at how many times each number will appear in the product.
$$1!\times2!\times3!\times...\times100!
=1^{100}\times2^{99}\times3^{98}\times...\times100^1$$
Now split the odd and even numbers.
$$=\left[1^{100}\times3^{98}\times...\times99^2\right]\times\left[2^{99}\times4^{97}\times...\times100^1\right]$$
As all the powers in the first bracket are even, the first bracket is a square number.
$$=\left[1^{50}\times3^{49}\times...\times99^1\right]^2\times\left[2^{99}\times4^{97}\times...\times100^1\right]$$
Next, take a factor of two out of each number in the second bracket.
$$=\left[1^{50}\times3^{49}\times...\times99^1\right]^2\times\left[(2\times1)^{99}\times(2\times2)^{97}\times...\times(2\times50)^1\right]$$
$$=\left[1^{50}\times3^{49}\times...\times99^1\right]^2\times2^{99+97+...+1}\left[1^{99}\times2^{97}\times...\times50^1\right]$$
$$=\left[1^{50}\times3^{49}\times...\times99^1\right]^2\times2^{2500}\left[1^{99}\times2^{97}\times...\times50^1\right]$$
The only odd powers involved are now in the last bracket. Dividing by \(50!\) would make each of these powers even, hence the overall number would be square.
$$\frac{1!\times2!\times3!\times...\times100!
}{50!}=\left[1^{50}\times3^{49}\times...\times99^1\right]^2\times2^{2500}\left[1^{98}\times2^{96}\times...\times50^0\right]$$
$$=\left[1^{50}\times3^{49}\times...\times99^1\times2^{1250}\times1^{49}\times2^{48}\times...\times50^0\right]^2$$
Extension
For which numbers \(m\) is it possible to find a number \(n\) such that $$\frac{1!\times2!\times...\times m!}{n!}$$ is a square number?
An arm and a leg
If 60% of people have lost an eye, 75% an ear, 80% an arm and 85% a leg, what is the least percentage of people that have lost all four?
Show answer
Hide answer
40% of people still have both eyes, 25% both ears, 20% both arms and 15% both legs. If none of these overlap, they add to 100%. Therefore at least 0% of people have lost all four.
Blackboard sums II
The numbers 1 to 20 are written on a blackboard. Each turn, you may erase two adjacent numbers, \(a\) and \(b\) (\(a\) is to the left of \(b\)) and write the difference \(a-b\)
in their place. You continue until only one number remains.
What is the largest number you can make?
Show answer & extension
Hide answer & extension
Erasing 2 and 3; then the result and 4; then the result and 5 and so on will lead to having \(1\) and \(2-\sum_{i=3}^{20}i\) on the board.
Erasing these will give \(1-2+\sum_{i=3}^{20}i=206\).
Extension
The numbers 1 to 20 are written on a blackboard. Each turn, you may erase two adjacent numbers, \(a\) and \(b\) (\(a\) is to the left of \(b\)) and write the quotient \(a/b\)
in their place. You continue until only one number remains.
What is the largest number you can make?
Powerful quadratics
Find all real solutions to
$$(x^2-7x+11)^{(x^2-11x+30)}=1.$$
Show answer
Hide answer
If \(x^2-7x+11=1\) or \(x^2-11x+30=0\), then this is one. The solutions to these are \(x=2,5,\) and \(6\).
It could also be one if \(x^2-7x+11=-1\) and \(x^2-11x+30\) is even. This happens when \(x=3\) or \(4\).
Therefore all the solutions to this are \(x=2,3,4,5\) or \(6\).
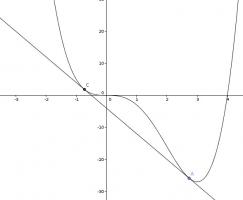
Two tangents
Find a line which is tangent to the curve \(y=x^4-4x^3\) at 2 points.
Show answer
Hide answer
At \(x=a\), \(y=a^4-4a^2\) and \(\frac{dy}{dx}=4a^3-12a^2\). Therefore the equation of the tangent at \(x=a\) will be \(y=(4a^3-12a^2)x+8a^3-3a^4\).
Taking this away from \(y=x^4-4x^3\) gives \(y=x^4-4x^3-(4a^3-12a^2)x-8a^3+3a^4\). We can now look at where this curve is tangent to \(y=0\) and look for a value of \(a\) that makes it tangent at two points.
If this curve is tangent to the \(x\)-axis at \(x=b\), then it will have a repeated root at \(x=b\). We know it is tangent at \(x=a\), so dividing \(x^4-4x^3-(4a^3-12a^2)x-8a^3+3a^4\) by \((x-a)\) twice gives \(x^2+(2a-4)x+3a^2-8a\). We want this to have a repeated root, hence the discriminant, \((2a-4)^2-4(3a^2-8a)\), must be 0.
Solving this gives \(a=1\pm\sqrt3\).
Therefore the equation of the line is \(y=-8x-4\).
Blackboard sums
The numbers 1 to 20 are written on a blackboard. Each turn, you may erase two numbers, \(a\) and \(b\) and write the sum \(a+b\) in their place. You continue until only one number remains.
What is the largest number you can make?
Show answer & extension
Hide answer & extension
After each turn, the total of the numbers written on the board remains the same. Therefore the sum of the numbers is always the same: 210
Extension
The numbers 1 to 20 are written on a blackboard. Each turn, you may erase two numbers, \(a\) and \(b\) and write the product \(a\times b\) in their place. You continue until only one number remains.
What is the largest number you can make?
Hat check
Three logicians, A, B and C, are wearing hats. Each has a strictly positive integer written on it. The number on one of the hats is the sum of the numbers on the other two.
The logicians say:
A: I don't know the number on my hat.
B: The number on my hat is 15.
Which numbers are on hats A and C?
Show answer
Hide answer
Each of the logicians can see two numbers and knows that her number is either the sum of or the difference between these numbers.
The only way in which A could've known her number was if B and C had the same number (as the difference would be 0, not positive). So after A speaks, B knows that B\(\not=\)C.
There are two ways in which B could know her number: (1) if A=C, or (2) if the information revealed by A removed one of the options.
(1) is not possible, as this would mean that B is the sum of A and C and therefore even (but 15 is odd.
Therefore (2) must have happened. Learning B\(\not=\)C removed one of B's options, so B=C must have been one of B's options. This is only possible if A=2C, giving B's options as being equal to C or 3C.
As B cannot be C, B must therefore be 3C, so the numbers are: A=10, B=15, C=5.