Puzzles
4 December
Today's number is a three digit number which is equal to the sum of the cubes of its digits. One less than today's number also has this property.
3 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number you can make with the digits in the red boxes.
| ÷ | - | = 3 | |||
| + | + | ÷ | |||
| ÷ | × | = 1 | |||
| × | - | + | |||
| - | × | = 20 | |||
| = 91 | = 6 | = 8 |
2 December
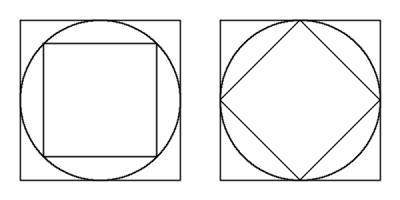
Carol draws a square with area 62. She then draws the smallest possible circle that this square is contained inside.
Next, she draws the smallest possible square that her circle is contained inside. What is the area of her second square?
1 December
It is possible to write 325 different numbers using the digits 1, 2, 3, 4, and 5 at most once each (and using no other digits).
How many of these numbers are odd?
Advent 2019 logic puzzle
It's nearly Christmas and something terrible has happened: while out on a test flight, Santa's sled was damaged and Santa, Rudolph and Blitzen fell to the ground over the Advent Isles.
You need to find Santa and his reindeer before Christmas is ruined for everyone.
You have gathered one inhabitant of the four largest Advent Isles—Rum, Land, Moon and County—and they are going to give you a series of clues about where Santa and his reindeer landed.
However, one or more of the islanders you have gathered may have been involved in damaging Santa's sled and causing it to crash: any islander involved in this will lie to you to attempt to stop
you from finding Santa and his reindeer.
Once you are ready to search for Santa, Rudolph and Blitzen, you can find the map by following this link.
Each of the clues will be about Santa's, Rudolph's or Blitzen's positions in Advent Standard Coordinates (ASC): ASC are given by six two-digit numbers with dots inbetween, for example
12.52.12.13.84.55.
For this example coordinate, the islanders will refer to
(the first) 12 as the first coordinate,
52 as the second coordinate,
(the second) 12 as the third coordinate,
13 as the fourth coordinate,
84 as the fifth coordinate, and
55 as the sixth coordinate.
Here are the clues:
3
Rum says: "The product of all the digits in Blitzen's six coords is 432."21
Moon says: "Blitzen's fifth coord is 23."9
Moon says: "Blitzen's third coord is 23."1
Land says: "Santa's third coord ends in 3, 0 or 1."2
Land says: "Santa's third coord ends in 2, 0 or 3."4
Rum says: "Santa's second coord ends in 3, 4 or 1."12
Rum says: "Rudolph's second and sixth coords are both 64."10
Rum says: "All six of Rudolph's coords are factors of 256."18
Moon says: "Santa's fourth and fifth coords are both 79."24
County says: "Santa's third coord ends in 3, 2 or 1."22
Land says: "Santa's sixth coord is not 43."7
Rum says: "Santa's sixth coord is 43."23
County says: "One of the digits of Santa's third coord is 7."25
✔14
Land says: "Santa's third coord is 12."5
Rum says: "Santa's first coord is 36."15
Rum says: "Blitzen's first coord is 23."17
Rum says: "The first digit of Santa's third coord is 1."8
County says: "Santa's third coord shares a factor (≠1) with 270."6
County says: "Santa's second coord is 21."16
Land says: "Blitzen's second coord is 21."20
Moon says: "All six of Rudolph's coords are multiples of 8."11
Moon says: "The sum of Rudolph's six coords is 192."13
Moon says: "Santa's second coord is 21 or 11."19
Moon says: "Blitzen's fourth and sixth coords are both 11."To find a point's ASC coordinates, split a map of the islands into a 9×9 grid, then number the rows and columns 1 to 9: the first two digits of ASC give the vertical then horizontal position of a square in this grid.
The next two digits then give a smaller square when this square is then itself split into a 9×9 grid, and so on. An example is show below.
You can view the map here.
24 December
There are six 3-digit numbers with the property that the sum of their digits is equal to the product of their digits. Today's number is the largest of these numbers.
23 December
Arrange the digits 1-9 in a 3×3 square so the 3-digits numbers formed in the rows and columns are the types of numbers given at the ends of the rows and columns.
The number in the first column is today's number.
| a multiple of 4 | |||
| a cube | |||
| a multiple of 3 | |||
| today's number | a cube | an odd number |
22 December
In bases 3 to 9, the number 112 is:
\(11011_3\),
\(1300_4\),
\(422_5\),
\(304_6\),
\(220_7\),
\(160_8\), and
\(134_9\).
In bases 3, 4, 6, 8 and 9, these representations contain no digit 2.
There are two 3-digit numbers that contain no 2 in their representations in all the bases between 3 and 9 (inclusive). Today's number is the smaller of these two numbers.