Puzzles
13 December
There are 6 ways to split the sequence of the numbers 1 to 5 into three shorter sequences:
- 1 and 2 and 3, 4, 5
- 1 and 2, 3 and 4, 5
- 1 and 2, 3, 4 and 5
- 1, 2 and 3 and 4, 5
- 1, 2 and 3, 4 and 5
- 1, 2, 3 and 4 and 5
Today's number is the number of ways to split the sequence of the numbers 1 to 10 into five shorter sequences.
Show answer
Hide answer
There are 9 gaps between the numbers 1 to 10. We need to pick 5 of these gaps to split the sequence. There are \(\left(\begin{array}{c}9\\5\end{array}\right)\) ways to do this:
this is 126.
12 December
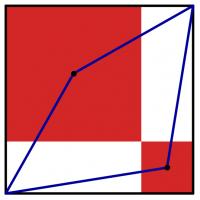
The diagram to the left shows a large black square. Inside this square, two red squares have been drawn.
(The sides of the red squares are parallel to the sides of the black square; each red square shares a vertex with the black square; and the two red squares share a vertex.)
A blue quadrilateral has then been drawn with vertices at two corners of the black square and the centres of the red squares.
The area of the blue quadrilateral is 167. What is the area of the black square?
Show answer
Hide answer
No matter the exact size of each square, the blue quadrilateral will always fill half the square, so the area of the square is 334.
11 December
Noel has a large pile of cards. Half of them are red, the other half are black. Noel splits the cards into two piles: pile A and pile B.
Two thirds of the cards in pile A are red. Noel then moves 108 red cards from pile A to pile B. After this move, two thirds of the cards in pile B are red.
How many cards did Noel start with?
Note: There was a mistake in the original version of today's puzzle. The number 21 has been replaced with 108.
Show answer
Hide answer
Let's say there were originally \(t\) cards of each colour, and \(2a\) red cards and \(a\) black cards in pile A.
After the move, there were \(t-2a+108\) red cards and \(t-a\) black cards in pile B. Two thirds of the card in pile B are red, so:
$$t-2a+108=2(t-a)$$
$$t=108$$
Therefore there were 108×2=216 cards.
Interestingly, it appears that this answer is independent of \(a\): any number of cards could be put in each pile and this situation would still work. However, only one situation could have happened
unless you allow there to at some points have been a negative number of cards in each pile.
10 December
Today's number is the smallest multiple of 24 whose digits add up to 24.
Show answer
Hide answer
There are one three-digit even numbers whose digits add to 24: 798, 888 and 996. Of these, only 888 is a multiple of 24.
9 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | | × | | = 54 |
| × | | + | | ÷ | |
| - | | ÷ | | = 1 |
| ÷ | | - | | × | |
| + | | - | | = 6 |
=
18 | | =
6 | | =
18 | |
Show answer
Hide answer
| 4 | + | 5 | × | 6 | = 54 |
| × | | + | | ÷ | |
| 9 | - | 8 | ÷ | 1 | = 1 |
| ÷ | | - | | × | |
| 2 | + | 7 | - | 3 | = 6 |
=
18 | | =
6 | | =
18 | |
The product of the numbers in the red boxes is 144.
8 December
The residents of Octingham have 8 fingers. Instead of counting in base ten, they count in base eight: the digits of their numbers represent ones, eights, sixty-fours, two-hundred-and-fifty-sixes, etc
instead of ones, tens, hundreds, thousands, etc.
For example, a residents of Octingham would say 12, 22 and 52 instead of our usual numbers 10, 18 and 42.
Today's number is what a resident of Octingham would call 11 squared (where the 11 is also written using the Octingham number system).
Show answer
Hide answer
The Octingham resident's 11 is equal to our number 9. 9 squared is 81. 81 in base eight is 121.
Interestingly, this is the same answer as "just" doing 11 squred in base ten.
7 December
There are 15 dominos that can be made using the numbers 0 to 4 (inclusive):
The sum of all the numbers on all these dominos is 60.
Today's number is the sum of all the numbers on all the dominos that can be made using the numbers 5 to 10 (inclusive).
Show answer
Hide answer
Each number will appear 7 times: one time paired with the numbers six numbers 5 to 10, plus an extra appearance on the tile containing the same number twice.
The total of all the numbers is therefore 7×(5+6+...+10)=7×45=315.
6 December
There are 12 ways of placing 2 tokens on a 2×4 grid so that no two tokens are next to each other horizonally, vertically or diagonally:
Today's number is the number of ways of placing 5 tokens on a 2×10 grid so that no two tokens are next to each other horizonally, vertically or diagonally.
Show answer
Hide answer
First, consider placing 5 tiles in a 1×9 grid. There is only one way to do this:
To get the number of ways of placing 5 tiles in a 1×10 grid, imagine adding an extra blank square to either the start or end of the grid or between two of the counters.
There are 6 places this tile could be inserted leading to 6 arrangements of 5 tiles in a 1×10 grid.
For 5 tiles in a 2×10 grid, you can first pick the columns the tiles go in (as a tile being in a column means nothing can be placed the columns either side, the number of ways to pick
columns is the same and the number of wats to arrange 5 tokens in a 1×10 grid). For each of these column choices, there are two locations for each tile (top or bottom).
This leads to a total number of arrangements of 6×25=192.
|