Sunday Afternoon Maths XXIV
Exact change
In the UK, the coins less than £1 are 1p, 2p, 5p, 10p, 20p and 50p. How many coins would I need to carry in my pocket so that I could make any value from 1p to 99p?
In the US, the coins less than $1 are 1¢, 5¢, 10¢, 25¢. How many coins would I need to carry in my pocket so that I could make any value from 1¢ to 99¢?
Show answer & extension
Hide answer & extension
In the UK, eight coins are needed: 1p, 1p, 2p, 5p, 10p, 20p, 20p, 50p.
In the US, ten coins are needed: 1¢, 1¢, 1¢, 1¢, 5¢, 10¢, 10¢, 25¢, 25¢, 25¢.
Extension
In a far away country, the unit of currency is the #, which is split into 100@ (# is like £ or $; @ is like p or ¢).
Let C be the number of coins less than #1. Let P be the number of coins needed to make any value between 1@ and 99@. Which coins should be the country mint to minimise the value of P+C?
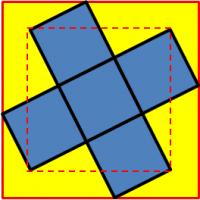
Square cross
A figure in the shape of a cross is made from five 1 x 1 squares, as shown. The cross is inscribed in a large square whose sides are parallel to the dashed square, formed by four vertices of the cross.
What is the area of the large outer square?
Show answer
Hide answer
The smaller diagonal square is made up of a 1×1 square and four 1×2 right-angled triangles. Therefore its area is 5.
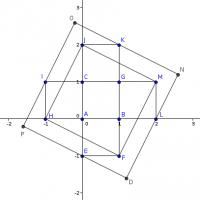
The line FM, and therefore the line DN, has gradient 2. The line JM, and therefore the line ON, has gradient -½. ON passes through (1,2) and DN passes through (2,0). Therefore, DN has equation \(y=2x-4\) and ON has equation \(y=\frac{5}{2}-\frac{1}{2}x\). These lines intersect at \((\frac{13}{5},\frac{6}{5})\), these are the co-ordinates of N. By the same method, the co-ordinates of P are \((-\frac{8}{5},-\frac{1}{5})\).
By Pythagoras' Theorem, The diagonal of the larger square is \(\frac{7\sqrt{10}}{5}\) and so the area of the larger square is 9.8.
![](javascript:showlimage("959058_orig.png"))
![](javascript:showlimage("cross+square.png"))