Sunday Afternoon Maths XVIII
Posted on 2014-06-22
Seven digits
"I'm thinking of a number. I've squared it. I've squared the square. And I've multiplied the second square by the original number. So I now have a number of seven digits whose final digit is a 7," said Dr. Dingo to his daughter.
Can you work out Dr. Dingo's number?
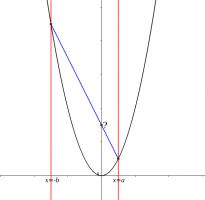
Parabola
Source: Alex Through the Looking-Glass: How Life Reflects Numbers and Numbers Reflect Life by Alex Bellos
On a graph of \(y=x^2\), two lines are drawn at \(x=a\) and \(x=-b\) (for \(a,b>0\). The points where these lines intersect the parabola are connected.
What is the y-coordinate of the point where this line intersects the y-axis?
If you enjoyed these puzzles, check out Advent calendar 2024,
puzzles about pascal's triangle, or a random puzzle.
puzzles about pascal's triangle, or a random puzzle.