Sunday Afternoon Maths LXIII

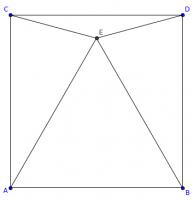
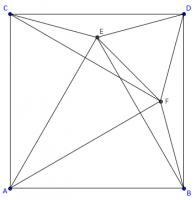
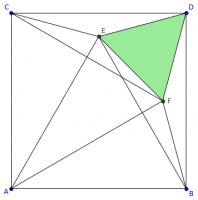
The triangle is equilateral.

To see why, add a copy of point \(E\) rotated by 90°. This is labelled \(F\) on the diagram below.

Angles \(BDE\) and \(CDF\) are both 75°. Therefore angles \(CDE\) and \(BDF\) are both 15°. This means that angle \(FDE\) is 60°.

Line \(AD\) is a line of symmetry of the diagram, so angles \(DFE\) and \(DEF\) are equal and both 60°. Therefore, triangle DEF is equilateral. This triangle is show in green in the diagram below.

Lines \(EF\), \(DF\) and \(BF\) are all equal length, so triangles \(BFE\) and \(BFD\) are isosceles. Angles \(BDF\) and \(FBD\) are both 15°. Angles \(FBE\) and \(FEB\) are equal, and the angles in triangle \(BED\) add to 180°: this means that angle \(FBE\) is 15°.

Angles \(FBE\) and \(FBD\) are both 15°, and so angle \(EBD\) is 30°. Angles \(EBD\) and \(ABE\) add to 90°, and so angle \(ABE\) is 60°.

By symmetry, angle \(BAE\) is also 60°. Angle \(BEA\) must therefore also be 60°, so triangle \(ABE\) is equilateral.

Consider the top, front, and right sides of the cube.

If the top number is \(a\) more than a multiple of six, then the front and right numbers must both be \(a\) less than a multiple of 6 (so that when added to the top number they make a multiple of 6). But when the front and right numbers are added, they make \(2a\) less than a multiple of 6; but this must also be a multiple of 6.

This is only possible if \(a=0\) or \(a=3\). So the numbers must be either all multiples of 6, or all 3 more than multiples of 6.

The smallest set of numbers that are all 3 more than multiples of 6 is 3,9,15,21,27,33. The sum of these is 108. The smallest set of numbers that are all multiples of 6 is the set with each number three more than these, so 108 is the smallest possible total.

Six numbers are written on the faces of a cube. The sum of the numbers on any two adjacent faces is a multiple of \(n\).

What is the smallest possible sum of the six numbers?