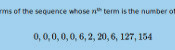Blog
2019-06-19
A308092 The sum of the first \(n\) terms of the sequence is the concatenation of the first \(n\) bits of the sequence read as binary, with \(a(1) = 1\).1, 2, 3, 7, 14, 28, 56, 112, 224, 448, 896, 1791, 3583, 7166, ...

To understand this definition, let's look at the first few terms of this sequence written in binary:
By "the concatenation of the first \(n\) bits of the sequence", it means the first \(n\) binary digits of the whole sequence written in order:
1, then 11, then 110, then 1101, then 11011, then 110111, and so on. So the definition means:
- The first term is 1, as given in the definition (\(a(1)=1\)).
- The sum of the first 2 terms is the first 2 digits: \(1+10=11\).
- The sum of the first 3 terms is the first 3 digits: \(1+10+11=110\).
- The sum of the first 4 terms is the first 4 digits: \(1+10+11+111=1101\).
- The sum of the first 5 terms is the first 5 digits: \(1+10+11+111+1110=11011\).
As we know that the sum of the first \(n-1\) terms is the first \(n-1\) digits, we can calculate the third term of this sequence onwards using:
"\(a(n)\) is the concatenation of the first \(n\) bits of the sequence subtract concatenation of the first \(n-1\) bits of the sequence":
- The third term is \(110 - 11 = 11\).
- The fourth term is \(1101 - 110 = 111\).
- The fourth term is \(11011 - 1101 = 1110\).
- The fifth term is \(110111 - 11011 = 11100\).
The conjecture
Peter's conjecture is that the number of 1s in each term is greater than or equal to the number of 1s in the previous term.
I'm going to prove this conjecture. If you'd like to have a try first, stop reading now and come back when you're ready for spoilers.
(If you'd like a hint, read the next section then pause again.)
Adding a digit
The third term of the sequence onwards can be calculated by subtracting the first \(n-1\) digits from the first \(n\) digits.
If the first \(n-1\) digits form a binary number \(x\), then the first \(n\) digits will be \(2x+d\), where \(d\) is the \(n\)th digit
(because moving all the digits to the left one place in binary is multiplying by two).
Therefore the different is \(2x+d-x=x+d\), and so we can work out the \(n\)th term of the sequence by adding the \(n\)th digit in the
sequence to the first \(n-1\) digits. (Hat tip to Martin Harris, who spotted this first.)
Carrying
Adding 1 to a binary number the ends in 1 will cause 1 to carry over to the left. This carrying will continue until the 1 is carried into
a position containing 0, and after this all the digits to the left of this 0 will remain unchanged.
Therefore adding a digit to
the first \(n-1\) digits can only change the digits from the rightmost 0 onwards.
Endings
We can therefore disregard all the digits before the rightmost 0, and look at how the \(n\)th term compares to the \((n-1)\)th term.
There are 5 ways in which the first \(n\) digits could end:
- \(00\)
- \(010\)
- \(01...10\) (where \(1...1\) is a string of 2 or more ones)
- \(01\)
- \(01...1\) (where \(1...1\) is again a string of 2 or more ones)
We now look at each of these in turn and show that the \(n\)th term will contain at least as many ones at the \((n-1)\)th term.
Case 1: \(00\)
If the first \(n\) digits of the sequence are \(x00\) (a binary number \(x\) followed by two zeros), then the \((n-1)\)th term of the
sequence is \(x+0=x\), and the \(n\)th term of the sequence is \(x0+0=x0\). Both \(x\) and \(x0\) contain the same number of ones.
Case 2: \(010\)
If the first \(n\) digits of the sequence are \(x010\), then the \((n-1)\)th term of the sequence is \(x0+1=x1\),
and the \(n\)th term of the sequence is \(x01+0=x01\). Both \(x1\) and \(x01\) contain the same number of ones.
Case 3: \(01...10\)
If the first \(n\) digits of the sequence are \(x01...10\), then the \((n-1)\)th term of the sequence is \(x01...1+1=x10...0\),
and the \(n\)th term of the sequence is \(x01...10+1=x01...1\). \(x01...1\) contains more ones than \(x10...0\).
Case 4: \(01\)
If the first \(n\) digits of the sequence are \(x01\), then the \((n-1)\)th term of the sequence is \(x+0=x\),
and the \(n\)th term of the sequence is \(x0+1=x1\). \(x1\) contains one more one than \(x\).
Case 5: \(01...1\)
If the first \(n\) digits of the sequence are \(x01...1\), then the \((n-1)\)th term of the sequence is \(x01...1+1=x10...0\),
and the \(n\)th term of the sequence is \(x01...1+1=x10...0\). Both these contain the same number of ones.
In all five cases, the \(n\)th term contains more ones or an equal number of ones to the \((n-1)\)th term, and so the conjecture is true.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-10-08
During my Electromagnetic Field talk this year, I spoke about @mathslogicbot, my Twitter bot that is working its way through the tautologies in propositional calculus. My talk included my conjecture that the number of tautologies of length \(n\) is an increasing sequence (except when \(n=8\)). After my talk, Henry Segerman suggested that I also look at the number of contradictions of length \(n\) to look for insights.
A contradiction is the opposite of a tautology: it is a formula that is False for every assignment of truth values to the variables. For example, here are a few contradictions:
$$\neg(a\leftrightarrow a)$$
$$\neg(a\rightarrow a)$$
$$(\neg a\wedge a)$$
$$(\neg a\leftrightarrow a)$$
The first eleven terms of the sequence whose \(n\)th term is the number of contradictions of length \(n\) are:
$$0, 0, 0, 0, 0, 6, 2, 20, 6, 127, 154$$
This sequence is A277275 on OEIS. A list of contractions can be found here.
For the same reasons as the sequence of tautologies, I would expect this sequence to be increasing. Surprisingly, it is not increasing for small values of \(n\), but I again conjecture that it is increasing after a certain point.
Properties of the sequences
There are some properties of the two sequences that we can show. Let \(a(n)\) be the number of tautolgies of length \(n\) and let \(b(n)\) be the number of contradictions of length \(n\).
First, the number of tautologies and contradictions, \(a(n)+b(n)\), (A277276) is an increasing sequence. This is due to the facts that \(a(n+1)\geq b(n)\) and \(b(n+1)\geq a(n)\), as every tautology of length \(n\) becomes a contraction of length \(n+1\) by appending a \(\neg\) to be start and vice versa.
This implies that for each \(n\), at most one of \(a\) and \(b\) can be decreasing at \(n\), as if both were decreasing, then \(a+b\) would be decreasing. Sadly, this doesn't seem to give us a way to prove the conjectures, but it is a small amount of progress towards them.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2015-08-29
A few weeks ago, I made OEISbot, a Reddit bot which posts information whenever an OEIS sequence is mentioned.
This post explains how OEISbot works. The full code can be found on GitHub.
Getting started
OEISbot is made in Python using PRAW (Python Reddit Api Wrapper). PRAW can be installed with:
bash
pip install prawBefore making a bot, you will need to make a Reddit account for your bot, create a Reddit app and obtain API keys. This python script can be used to obtain the necessary keys.
Once you have your API keys saved in your praw.ini file, you are ready to make a bot.
Writing the bot
First, the necessary imports are made, and test mode is activated if the script is run with test as an argument. We also define an exception that will be used later to kill the script once it makes a comment.
python
import prawimport re
import urllib
import json
from praw.objects import MoreComments
import sys
test = False
if len(sys.argv) > 1 and sys.argv[1] == "test":
test = True
print("TEST MODE")
class FoundOne(BaseException):
pass
To prevent OEISbot from posting multiple links to the same sequence in a thread, lists of sequences linked to in each thread can be loaded and saved using the following functions.
python
def save_list(seen, _id):print(seen)
with open("/home/pi/OEISbot/seen/"+_id, "w") as f:
return json.dump(seen, f)
def open_list(_id):
try:
with open("/home/pi/OEISbot/seen/" + _id) as f:
return json.load(f)
except:
return []
The following function will search a post for a mention of an OEIS sequence number.
python
def look_for_A(id_, text, url, comment):seen = open_list(id_)
re_s = re.findall("A([0-9]{6})", text)
re_s += re.findall("oeis\.org/A([0-9]{6})", url)
if test:
print(re_s)
post_me = []
for seq_n in re_s:
if seq_n not in seen:
post_me.append(markup(seq_n))
seen.append(seq_n)
if len(post_me) > 0:
post_me.append(me())
comment(joiner().join(post_me))
save_list(seen, id_)
raise FoundOne
The following function will search a post for a comma-separated list of numbers, then search for it on the OEIS. If there are 14 sequences or less found, it will reply. If it finds a list with no matches on the OEIS, it will message /u/PeteOK, as he likes hearing about possibly new sequences.
python
def look_for_ls(id_, text, comment, link, message):seen = open_list(id_)
if test:
print(text)
re_s = re.findall("([0-9]+\, *(?:[0-9]+\, *)+[0-9]+)", text)
if len(re_s) > 0:
for terms in ["".join(i.split(" ")) for i in re_s]:
if test:
print(terms)
if terms not in seen:
seen.append(terms)
first10, total = load_search(terms)
if test:
print(first10)
if len(first10)>0 and total <= 14:
if total == 1:
intro = "Your sequence (" + terms \
+ ") looks like the following OEIS sequence."
else:
intro = "Your sequence (" + terms + \
+ ") may be one of the following OEIS sequences."
if total > 4:
intro += " Or, it may be one of the " + str(total-4) \
+ " other sequences listed [here]" \
"(http://oeis.org/search?q=" + terms + ")."
post_me = [intro]
if test:
print(first10)
for seq_n in first10[:4]:
post_me.append(markup(seq_n))
seen.append(seq_n)
post_me.append(me())
comment(joiner().join(post_me))
save_list(seen, id_)
raise FoundOne
elif len(first10) == 0:
post_me = ["I couldn't find your sequence (" + terms \
+ ") in the [OEIS](http://oeis.org). "
"You should add it!"]
message("PeteOK",
"Sequence not in OEIS",
"Hi Peter, I've just found a new sequence (" \
+ terms + ") in [this thread](link). " \
"Please shout at /u/mscroggs to turn the " \
"feature off if its spamming you!")
post_me.append(me())
comment(joiner().join(post_me))
save_list(seen, id_)
raise FoundOne
def load_search(terms):
src = urllib.urlopen("http://oeis.org/search?fmt=data&q="+terms).read()
ls = re.findall("href=(?:'|\")/A([0-9]{6})(?:'|\")", src)
try:
tot = int(re.findall("of ([0-9]+) results found", src)[0])
except:
tot = 0
return ls, tot
The markup function loads the necessary information from OEIS and formats it. Each comment will end with the output of the me function. The ouput of joiner will be used between sequences which are mentioned.
python
def markup(seq_n):pattern = re.compile("%N (.*?)<", re.DOTALL|re.M)
desc = urllib.urlopen("http://oeis.org/A" + seq_n + "/internal").read()
desc = pattern.findall(desc)[0].strip("\n")
pattern = re.compile("%S (.*?)<", re.DOTALL|re.M)
seq = urllib.urlopen("http://oeis.org/A" + seq_n + "/internal").read()
seq = pattern.findall(seq)[0].strip("\n")
new_com = "[A" + seq_n + "](http://oeis.org/A" + seq_n + "/): "
new_com += desc + "\n\n"
new_com += seq + "..."
return new_com
def me():
return "I am OEISbot. I was programmed by /u/mscroggs. " \
"[How I work](http://mscroggs.co.uk/blog/20). " \
"You can test me and suggest new features at /r/TestingOEISbot/."
def joiner():
return "\n\n- - - -\n\n"
Next, OEISbot logs into Reddit.
python
r = praw.Reddit("OEIS link and description poster by /u/mscroggs.")access_i = r.refresh_access_information(refresh_token=r.refresh_token)
r.set_access_credentials(**access_i)
auth = r.get_me()
The subs which OEISbot will search through are listed. I have used all the math(s) subs which I know about, as these will be the ones mentioning sequences.
python
subs = ["TestingOEISbot","math","mathpuzzles","casualmath","theydidthemath","learnmath","mathbooks","cheatatmathhomework","matheducation",
"puremathematics","mathpics","mathriddles","askmath",
"recreationalmath","OEIS","mathclubs","maths"]
if test:
subs = ["TestingOEISbot"]
For each sub OEISbot is monitoring, the hottest 10 posts are searched through for mentions of sequences. If a mention is found, a reply is generated and posted, then the FoundOne exception will be raised to end the code.
python
try:for sub in subs:
print(sub)
subreddit = r.get_subreddit(sub)
for submission in subreddit.get_hot(limit = 10):
if test:
print(submission.title)
look_for_A(submission.id,
submission.title + "|" + submission.selftext,
submission.url,
submission.add_comment)
look_for_ls(submission.id,
submission.title + "|" + submission.selftext,
submission.add_comment,
submission.url,
r.send_message)
flat_comments = praw.helpers.flatten_tree(submission.comments)
for comment in flat_comments:
if ( not isinstance(comment, MoreComments)
and comment.author is not None
and comment.author.name != "OEISbot" ):
look_for_A(submission.id,
re.sub("\[[^\]]*\]\([^\)*]\)","",comment.body),
comment.body,
comment.reply)
look_for_ls(submission.id,
re.sub("\[[^\]]*\]\([^\)*]\)","",comment.body),
comment.reply,
submission.url,
r.send_message)
except FoundOne:
pass
Running the code
I put this script on a Raspberry Pi which runs it every 10 minutes (to prevent OEISbot from getting refusals for posting too often). This is achieved with a cron job.
bash
*/10 * * * * python /path/to/bot.pyMaking your own bot
The full OEISbot code is available on GitHub. Feel free to use it as a starting point to make your own bot! If your bot is successful, let me know about it in the comments below or on Twitter.
Edit: Updated to describe the latest version of OEISbot.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2015-03-15
A few months ago, I set
@mathslogicbot (and @logicbot@mathstodon.xyz) going on the
long task of tweeting all the tautologies (containing 140 characters or less)
in propositional calculus with the symbols \(\neg\) (not), \(\rightarrow\)
(implies), \(\leftrightarrow\) (if and only if), \(\wedge\) (and) and \(\vee\)
(or). My first post on logic bot contains a full
explanation of propositional calculus, formulae and tautologies.
An alternative method
Since writing the original post, I have written an alternative script to
generate all the tautologies.
In this new method, I run through all possible strings of length 1 made
with character in the logical language, then strings of length 2, 3 and so on.
The script then checks if they are valid formulae and, if so, if they are
tautologies.
In the new script, only formulae where the first appearances of variables
are in alphabetical order are considered. This means that duplicate tautologies
are removed. For example, \((b\rightarrow(b\wedge a))\) will now be counted as
it is the same as \((a\rightarrow(a\wedge b))\).
You can view or download this alternative code on
github.
All the terms of the sequence that I have calculated so far can be viewed
here and the tautologies for these terms are
here.
Sequence
One advantage of this method is that it generates the tautologies sorted by
the number of symbols they contain, meaning we can generate the sequence whose
\(n\)th term is the number of tautologies of length \(n\).
The first ten terms of this sequence are
$$0, 0, 0, 0, 2, 2, 12, 6, 57, 88$$
as there are no tautologies of length less than 5; and, for example two
tautologies of length 6 (\((\neg a\vee a)\) and \((a\vee \neg a)\)).
This sequence is listed as
A256120 on OEIS.
Properties
There are a few properties of this sequence that can easily be shown.
Throughout this section I will use \(a_n\) to represent the \(n\)th
term of the sequence.
Firstly, \(a_{n+2}\geq a_n\). This can be explained as follows: let \(A\)
be a tautology of length \(n\). \(\neg\neg A\) will be of length \(n+2\) and
is logically equivalent to \(A\).
Another property is \(a_{n+4}\geq 2a_n\): given a tautology \(A\) of length
\(n\), both \((a\vee A)\) and \((A\vee a)\) will be tautologies of length
\(n+4\). Similar properties could be shown for \(\rightarrow\),
\(\leftrightarrow\) and \(\wedge\).
Given properties like this, one might predict that the sequence will be
increasing (\(a_{n+1}\geq a_n\)). However this is not true as \(a_7\) is 12
and \(a_8\) is only 6. It would be interesting to know at how many points in
the sequence there is a term that is less than the previous one. Given the
properties above it is reasonable to conjecture that this is the only one.
Edit: The sequence has been published on OEIS!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment