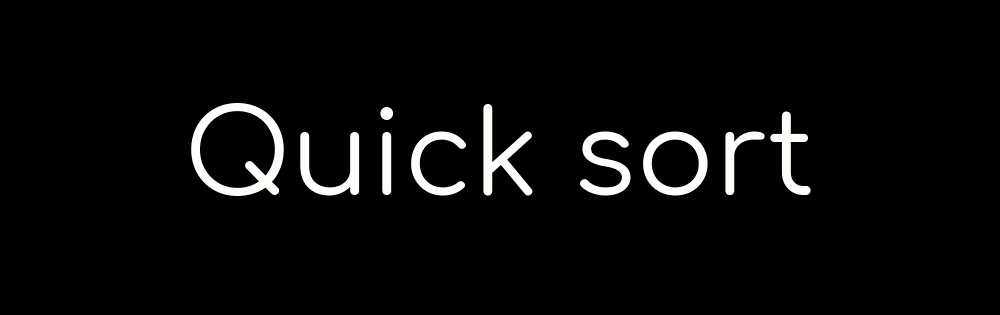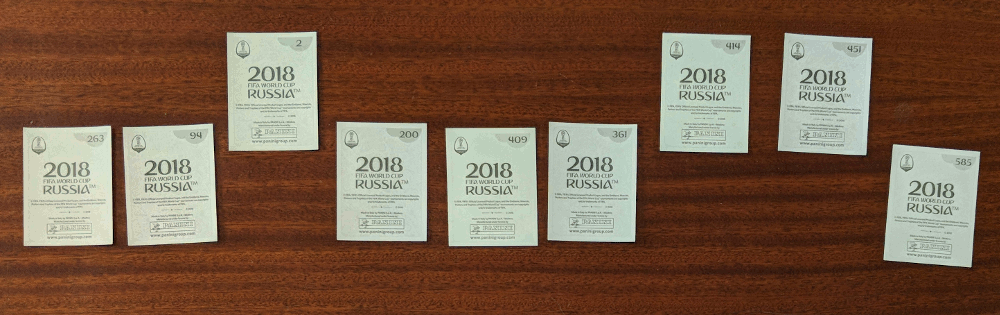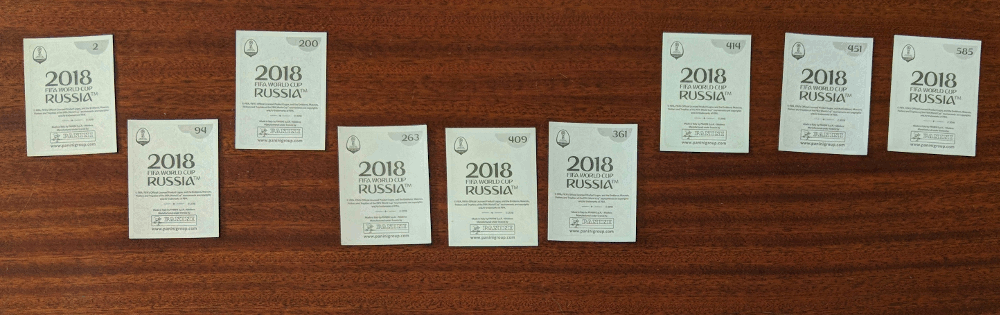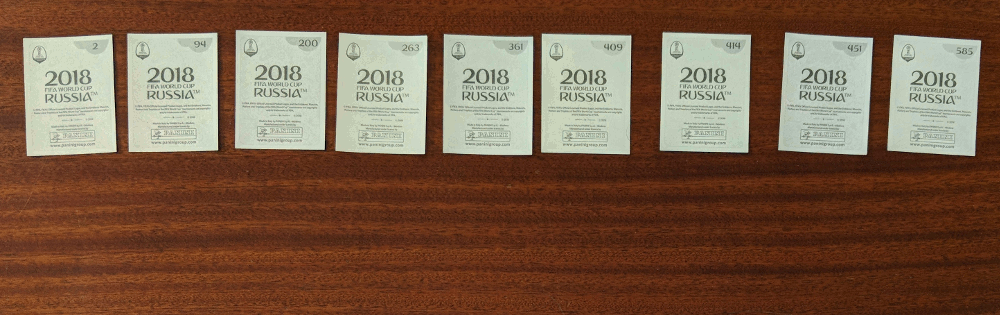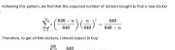Blog
World Cup stickers 2018, pt. 3
2018-07-07
So you've calculated how much you should expect the World Cup sticker book to cost
and recorded how much it actually cost. You might be wondering what else you can do with your sticker book.
If so, look no further: this post contains 5 mathematical things involvolving your sticker book and stickers.
Test the birthday paradox
![](javascript:showlimage("birthdaysbrazil.jpg"))
Stickers 354 and 369: Alisson and Roberto Firmino
In a group of 23 people, there is a more than 50% chance that two of them will share a birthday. This is often called the birthday paradox, as the number 23 is surprisingly small.
Back in 2014 when Alex Bellos suggested testing the birthday paradox on World Cup squads, as there are 23 players in a World Cup squad. I recently discovered that even further back in 2012, James Grime made a video about the birthday paradox in football games, using the players on both teams plus the referee to make 23 people.
In this year's sticker book, each player's date of birth is given above their name, so you can use your sticker book to test it out yourself.
Kaliningrad
![](javascript:showlimage("kaliningrad.jpg"))
Sticker 022: Kaliningrad
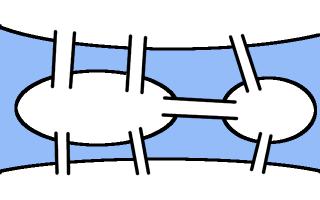
One of the cities in which games are taking place in this World Cup is Kaliningrad. Before 1945, Kaliningrad was called Königsberg. In Königsburg, there were seven bridges connecting four islands. The arrangement of these bridges is shown below.
![](javascript:showlimage("7bridges.png"))
The people of Königsburg would try to walk around the city in a route that crossed each bridge exactly one. If you've not tried this puzzle before, try to find such a route now before reading on...
In 1736, mathematician Leonhard Euler proved that it is in fact impossible to find such a route. He realised that for such a route to exist, you need to be able to pair up the bridges on each island so that you can enter the island on one of each pair and leave on the other. The islands in Königsburg all have an odd number of bridges, so there cannot be a route crossing each bridge only once.
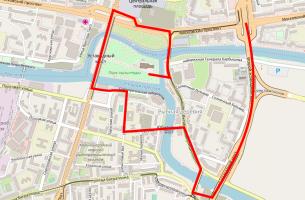
In Kaliningrad, however, there are eight bridges: two of the original bridges were destroyed during World War II, and three more have been built. Because of this, it's now possible to walk around the city crossing each bridge exactly once.
![](javascript:showlimage("kaliningrad-path.png"))
A route around Kaliningrad crossing each bridge exactly once.
I wrote more about this puzzle, and using similar ideas to find the shortest possible route to complete a level of Pac-Man, in this blog post.
Sorting algorithms
If you didn't convince many of your friends to join you in collecting stickers, you'll have lots of swaps. You can use these to practice performing your favourite sorting algorithms.
Bubble sort
In the bubble sort, you work from left to right comparing pairs of stickers. If the stickers are in the wrong order, you swap them. After a few passes along the line of stickers, they will be in order.
![](javascript:showlimage("bubble-sort-stickers.gif"))
Bubble sort
Insertion sort
In the insertion sort, you take the next sticker in the line and insert it into its correct position in the list.
![](javascript:showlimage("insertion-sort-stickers.gif"))
Insertion sort
Quick sort
In the quick sort, you pick the middle sticker of the group and put the other stickers on the correct side of it. You then repeat the process with the smaller groups of stickers you have just formed.
![](javascript:showlimage("quick-sort-stickers.gif"))
Quick sort
The football
![](javascript:showlimage("correct-football.jpg"))
Sticker 007: The official ball
Sticker 007 shows the official tournament ball. If you look closely (click to enlarge), you can see that the ball is made of a mixture of pentagons and hexagons. The ball is not made of only hexagons, as road signs in the UK show.
Stand up mathematician Matt Parker started a petition to get the symbol on the signs changed, but the idea was rejected.
If you have a swap of sticker 007, why not stick it to a letter to your MP about the incorrect signs as an example of what an actual football looks like.
Psychic pets
Speaking of Matt Parker, during this World Cup, he's looking for psychic pets that are able to predict World Cup results. Why not use your swaps to label two pieces of food that your pet can choose between to predict the results of the remaining matches?
![](javascript:showlimage("timber-football1.jpg"))
![](javascript:showlimage("timber-football2.jpg"))
Timber using my swaps to wrongly predict the first match
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2019-06-19
@Matthew: Thank you for the calculations. Good job I ordered the stickers I wanted #IRN. 2453 stickers - that's more than the number you bought (1781) to collect all stickers!Milad
@Matthew: Here is how I calculated it:
You want a specific set of 20 stickers. Imagine you have already \(n\) of these. The probability that the next sticker you buy is one that you want is
$$\frac{20-n}{682}.$$
The probability that the second sticker you buy is the next new sticker is
$$\mathbb{P}(\text{next sticker is not wanted})\times\mathbb{P}(\text{sticker after next is wanted})$$
$$=\frac{662+n}{682}\times\frac{20-n}{682}.$$
Following the same method, we can see that the probability that the \(i\)th sticker you buy is the next wanted sticker is
$$\left(\frac{662+n}{682}\right)^{i-1}\times\frac{20-n}{682}.$$
Using this, we can calculate the expected number of stickers you will need to buy until you find the next wanted one:
$$\sum_{i=1}^{\infty}i \left(\frac{20-n}{682}\right) \left(\frac{662+n}{682}\right)^{i-1} = \frac{682}{20-n}$$
Therefore, to get all 682 stickers, you should expect to buy
$$\sum_{n=0}^{19}\frac{682}{20-n} = 2453 \text{ stickers}.$$
You want a specific set of 20 stickers. Imagine you have already \(n\) of these. The probability that the next sticker you buy is one that you want is
$$\frac{20-n}{682}.$$
The probability that the second sticker you buy is the next new sticker is
$$\mathbb{P}(\text{next sticker is not wanted})\times\mathbb{P}(\text{sticker after next is wanted})$$
$$=\frac{662+n}{682}\times\frac{20-n}{682}.$$
Following the same method, we can see that the probability that the \(i\)th sticker you buy is the next wanted sticker is
$$\left(\frac{662+n}{682}\right)^{i-1}\times\frac{20-n}{682}.$$
Using this, we can calculate the expected number of stickers you will need to buy until you find the next wanted one:
$$\sum_{i=1}^{\infty}i \left(\frac{20-n}{682}\right) \left(\frac{662+n}{682}\right)^{i-1} = \frac{682}{20-n}$$
Therefore, to get all 682 stickers, you should expect to buy
$$\sum_{n=0}^{19}\frac{682}{20-n} = 2453 \text{ stickers}.$$
Matthew
@Matthew: Yes, I would like to know how you work it out please. I believe I have left my email address in my comment. It seems like a lot of stickers if you are just interested in one team.
Milad
@Milad: Following a similiar method to this blog post, I reckon you'd expect to buy 2453 stickers (491 packs) to get a fixed set of 20 stickers. Drop me an email if you want me to explain how I worked this out.
Matthew
Thanks for the maths, but I have one probability question. How many packs would I have to buy, on average, to obtain a fixed set of 20 stickers?
Milad
Add a Comment