Blog
Is MEDUSA the new BODMAS?
2017-01-13
I wrote this post with, and after much discussion with Adam Townsend. It also appeared on the Chalkdust Magazine blog.
Recently, Colin "IceCol" Beveridge blogged about something that's been irking him for a while: those annoying social media posts that tell you to work out a sum, such as \(3-3\times6+2\), and state that only $n$% of people will get it right (where \(n\) is quite small). Or as he calls it "fake maths".
![](javascript:showlimage("fake-maths.jpg"))
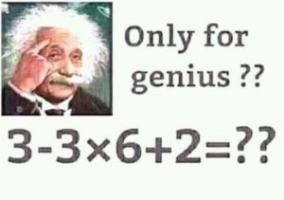
A classic example of "fake maths".
This got me thinking about everyone's least favourite primary school acronym: BODMAS (sometimes known as BIDMAS, or PEMDAS if you're American). As I'm sure you've been trying to forget, BODMAS stands for "Brackets, (to the power) Of, Division, Multiplication, Addition, Subtraction" and tells you in which order the operations should be performed.
Now, I agree that we all need to do operations in the same order (just imagine trying to explain your working out to someone who uses BADSOM!) but BODMAS isn't the order mathematicians use. It's simply wrong. Take the sum \(4-3+1\) as an example. Anyone can tell you that the answer is 2. But BODMAS begs to differ: addition comes first, giving 0!
The problem here is that in reality, we treat addition and subtraction as equally important, so sums involving just these two operations are calculated from left-to-right. This caveat is quite a lot more to remember on top of BODMAS, but there's actually no need: Doing all the subtractions before additions will always give you the same answer as going from left-to-right. The same applies to division and multiplication, but luckily these two are in the correct order already in BODMAS (but no luck if you're using PEMDAS).
So instead of BODMAS, we should be using BODMSA. But that's unpronounceable, so instead we suggest that from now on you use MEDUSA. That's right, MEDUSA:
- Mabano (brackets in Swahili)
- Exponentiation
- Division
- Ukubuyabuyelela (multiplication in Zulu)
- Subtraction
- Addition
This is big news. MEDUSA vs BODMAS could be this year's pi vs tau... Although it's not actually the biggest issue when considering sums like \(3-3\times6+2\).
The real problem with \(3-3\times6+2\) is that it is written in a purposefully confusing and ambiguous order. Compare the following sums:
$$3-3\times6+2$$ $$3+2-3\times6$$ $$3+2-(3\times6)$$
In the latter two, it is much harder to make a mistake in the order of operations, because the correct order is much closer to normal left-to-right reading order, helping the reader to avoid common mistakes. Good mathematics is about good communication, not tricking people. This is why questions like this are "fake maths": real mathematicians would never ask them. If we take the time to write clearly, then I bet more than \(n\)% of people will be able get the correct answer.
×1 ×1 ×1 ×1 ×1(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2017-11-27
We use BEDMAS in Canada (Brackets, Exponents, Division, Multiplication, Addition, Subtraction) But we are taught that you do whichever comes first from left to right if they are the addition/ subtraction or multiplication/division. So it could also be BEMDAS, or BEMDSA, or BEDMSA. It just uses the order the that rolls off the tongue more.Brodaha
×1 ×1 ×1 ×1 ×1 we use BOMAL - Brackets, Overs, Multiplication/Division, Addition/Subtraction, Left to Right. I agree they need to know negative numbers to fully understand and use BODMAS, BIDMAS, BEDMAS, PODMAS, PIDMAS, PEDMAS, BOMAL or MEDUSA×1 ×1 ×1 ×1 ×1
tiny
×1 ×1 ×1 ×1 ×1 If we could just teach young children about positive and negative numbers, then this wouldn't be a problem. Subtraction is just the addition of negative numbers. Division is also the multiplication of fractions. This is why BOMA/PEMA is the optimal method. I think MEDUSA is very creative, though.×1 ×1 ×1 ×1 ×1
Blan
×1 ×1 ×1 ×1 ×1 Add a Comment