Blog
Tube map Platonic solids, pt. 2
2012-11-02
This is the second post in a series of posts about tube map folding.
Following my previous post, I did a little more folding.
The post was linked to on Going Underground's Blog where it received this comment:
![](javascript:showlimage("rhombiwhy.png"))
In response to which I made this from 48 tube maps:
![](javascript:showlimage("rhombi.jpg"))
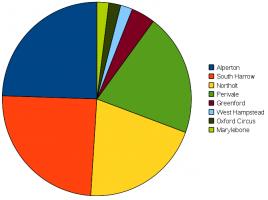
Also since the last post, I left 49 tetrahedrons at tube stations in a period of just over two weeks. Here's a pie chart showing which stations I left them at:
![](javascript:showlimage("leftpie.png"))
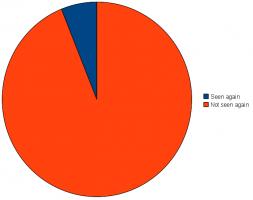
Of these 49, only three were still there the next time I passed through the station:
![](javascript:showlimage("pieagain.png"))
Due to the very low recapture rate, little more analysis can be done. Although I do wonder where they all ended up. Do you work at one of those stations and threw some away? Or did you pass through a station and pick one up? Or was it aliens and ghosts?
For my next trick, I want to gather a team of people, pick a day, and leave one at every station that day. If you want to join me, comment on this post, tweet me or comment on reddit and we can formulate a plan. Including your nearest station(s) in your message will help us sort out who takes which stations...
Previous post in series
This is the second post in a series of posts about tube map folding.
Next post in series
×1 ×4 ×4 ×1 ×1(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment