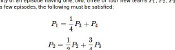Blog
Countdown probability
2014-04-06
On Countdown, contestants have to make words from nine letters. The contestants take turns to choose how many vowels and consonants they would like. This got me wondering which was the best combination to pick in order to get a nine letter word.
Assuming the letters in countdown are still distributed like this, the probability of getting combinations of letters can be calculated. As the probability throughout the game is dependent on which letters have been picked, I have worked out the probability of getting a nine letter word on the first letters game.
The probability of YODELLING
YODELLING has three vowels and six consonants. There are 6 (3!) ways in which the vowels could be ordered and 720 (6!) ways in which the consonants can be ordered, although each is repeated at there are two Ls, so there are 360 distinct ways to order the consonants. The probability of each of these is:
$$\frac{21\times 13\times 13\times 6\times 3\times 5\times 4\times 8\times 1}{67\times 66\times 65\times 74\times 73\times 72\times 71\times 70\times 69}$$
So the probability of getting YODELLING is:
$$\frac{6\times 360\times 21\times 13\times 13\times 6\times 3\times 5\times 4\times 8\times 1}{67\times 66\times 65\times 74\times 73\times 72\times 71\times 70\times 69} = 0.000000575874154$$
The probability of any nine letter word
I got my computer to find the probability of every nine letter word and found the following probabilities:
| Consonants | Vowels | Probability of nine letter word |
| 0 | 9 | 0 |
| 1 | 8 | 0 |
| 2 | 7 | 0 |
| 3 | 6 | 0.000546 |
| 4 | 5 | 0.019724 |
| 5 | 4 | 0.076895 |
| 6 | 3 | 0.051417 |
| 7 | 2 | 0.005662 |
| 8 | 1 | 0.000033 |
| 9 | 0 | 0 |
So the best way to get a nine letter word in the first letters game is to pick five consonants and four vowels.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment