Puzzles
23 December
I draw the parabola \(y=x^2\) and mark points on the parabola at \(x=17\) and \(x=-6\).
I then draw a straight line connecting these two points.
At which value of \(y\) does this line intercept the \(y\)-axis?
19 December
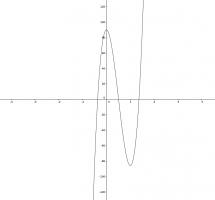
The equation \(352x^3-528x^2+90=0\) has three distinct real-valued solutions.
Today's number is the number of integers \(a\) such that the equation
\(352x^3-528x^2+a=0\) has three distinct real-valued solutions.
Show answer
Hide answer
The function \(f(x)=352x^3-528x^2+a\) with \(a=90\) looks like this (click to enlarge):
Adjusting the value of \(a\) will move the curve up and down. The equation \(f(x)=0\) will have three distinct solutions as long as the local minimum is below the \(x\)-axis
and the local maximum is above the \(x\)-axis.
The minimum and maximum are at \(x=1\) and \(x=0\). The difference between \(f(1)\) and \(f(0)\) is 176. This means that there are 175 possible integer values of \(a\) (as the endpoints are not included).
10 December
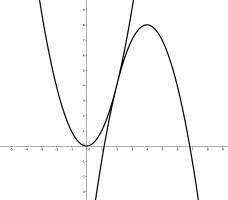
For all values of \(x\), the function \(f(x)=ax+b\) satisfies
$$8x-8-x^2\leqslant f(x)\leqslant x^2.$$
What is \(f(65)\)?
Edit: The left-hand quadratic originally said \(8-8x-x^2\). This was a typo and has now been corrected.
Show answer
Hide answer
If we plot the two quadratics, we see that they meet at \(x=2\) where they both have gradient 4.
The line \(f(x)\) must therefore pass through the point \((2,4)\) and have gradient 4, so its equation is \(f(x)=4x-4\).
This means that \(f(65)\) is 256.
6 December
\(p(x)\) is a quadratic with real coefficients. For all real numbers \(x\),
$$x^2+4x+14\leq p(x)\leq 2x^2+8x+18$$
\(p(2)=34\). What is \(p(6)\)?
Two tangents
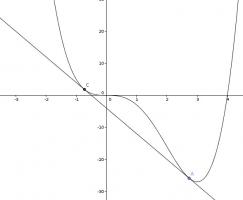
Find a line which is tangent to the curve \(y=x^4-4x^3\) at 2 points.
Show answer
Hide answer
At \(x=a\), \(y=a^4-4a^2\) and \(\frac{dy}{dx}=4a^3-12a^2\). Therefore the equation of the tangent at \(x=a\) will be \(y=(4a^3-12a^2)x+8a^3-3a^4\).
Taking this away from \(y=x^4-4x^3\) gives \(y=x^4-4x^3-(4a^3-12a^2)x-8a^3+3a^4\). We can now look at where this curve is tangent to \(y=0\) and look for a value of \(a\) that makes it tangent at two points.
If this curve is tangent to the \(x\)-axis at \(x=b\), then it will have a repeated root at \(x=b\). We know it is tangent at \(x=a\), so dividing \(x^4-4x^3-(4a^3-12a^2)x-8a^3+3a^4\) by \((x-a)\) twice gives \(x^2+(2a-4)x+3a^2-8a\). We want this to have a repeated root, hence the discriminant, \((2a-4)^2-4(3a^2-8a)\), must be 0.
Solving this gives \(a=1\pm\sqrt3\).
Therefore the equation of the line is \(y=-8x-4\).
Between quadratics
\(p(x)\) is a quadratic polynomial with real coefficients. For all real numbers \(x\),
$$x^2-2x+2\leq p(x)\leq 2x^2-4x+3$$
\(p(11)=181\). Find \(p(16)\).
Show answer
Hide answer
$$x^2-2x+2=(x-1)^2+1$$
$$2x^2-4x+3=2(x-1)^2+1$$
Therefore the minimum point of both of these quadratics is \((1,1)\). \(p(x)\) will only be between these if:
$$p(x)=a(x-1)^2+1\quad\text{where }1\leq a\leq 2$$
We know that \(p(11)=181\), so:
$$\begin{array}{rl}
181&=p(11)\\
&=a(11-1)^2+1\\
&=100a+1
\end{array}$$
Therefore \(a=1.8\). This means that:
$$\begin{array}{rl}
p(16)&=1.8(16-1)^2+1\\
&=1.8\times225+1\\
&=406
\end{array}$$
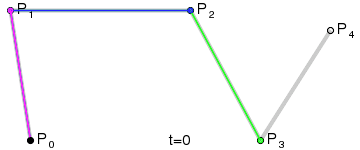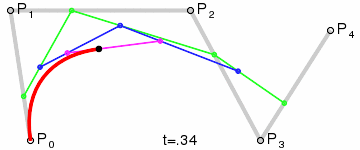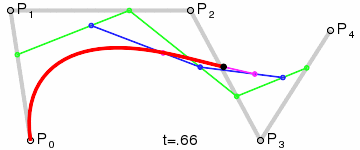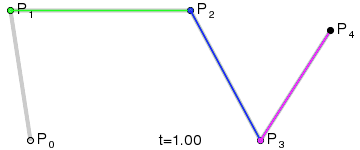
Bézier curve
1) A set of points \(P_0\), ..., \(P_n\) are chosen (in the example \(n=4\)).
2) A set of points \(Q_0\), ..., \(Q_{n-1}\) are defined by \(Q_i=t P_{i+1}+(1-t) P_i\) (shown in green).
3) A set of points \(R_0\), ..., \(R_{n-2}\) are defined by \(R_i=t Q_{i+1}+(1-t) Q_i\) (shown in blue).
.
.
.
\(n\)) After repeating the process \(n\) times, there will be one point. The Bézier curve is the path traced by this point at \(t\) varies between 0 and 1.
What is the Cartesian equation of the curve formed when:
$$P_0=\left(0,1\right)$$
$$P_1=\left(0,0\right)$$
$$P_2=\left(1,0\right)$$
Show answer & extension
Hide answer & extension
If
$$P_0=\left(0,1\right)$$
$$P_1=\left(0,0\right)$$
$$P_2=\left(1,0\right)$$
then
$$Q_0=t\left(0,0\right)+(1-t)\left(0,1\right)=\left(0,1-t\right)$$
$$Q_1=t\left(1,0\right)+(1-t)\left(0,0\right)=\left(t,0\right)$$
and so
$$R_0=t\left(t,0\right)+(1-t)\left(0,1-t\right)=\left(t^2,(1-t)^2\right)$$
which means that
$$x=t^2$$$$y=(1-t)^2$$
or
$$y=(1-\sqrt{x})^2$$
Extension
What should \(P_0\), \(P_1\) and \(P_2\) be to get a curve with Cartesian equation
$$y=(1-\sqrt{2x})^2$$
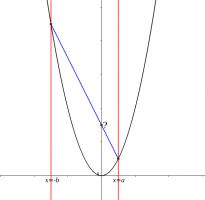
Parabola
On a graph of \(y=x^2\), two lines are drawn at \(x=a\) and \(x=-b\) (for \(a,b>0\). The points where these lines intersect the parabola are connected.
What is the y-coordinate of the point where this line intersects the y-axis?
Show answer & extension
Hide answer & extension
The co-ordinates of the points where the lines intersect the parabola are \((a,a^2)\) and \((-b,b^2)\). Hence the gradient of the line between them is:
$$\frac{a^2-b^2}{a-(-b)}=\frac{(a+b)(a-b)}{a+b}=a-b$$
Therefore the y-coordinate is:
$$b^2 + b(a-b) = ba$$
Ferdinand Möbius, who discovered this property called the curve a Multiplicationsmaschine or 'multiplication machine' as it could be used to perform multiplication.
Extension
How could you use the graph of \(y=x^2\) to divide 100 by 7?