Puzzles
1 December
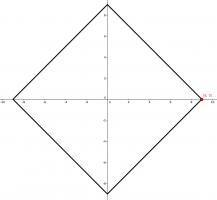
One of the vertices of a rectangle is at the point \((9, 0)\). The \(x\)-axis and \(y\)-axis are both lines of symmetry of the rectangle.
What is the area of the rectangle?
Show answer
Hide answer
The only way this is possible is if the rectangle is this square:
The area of this square is 162.
2009
2009 unit cubes are glued together to form a cuboid. A pack, containing 2009 stickers, is opened, and there are enough stickers to place 1 sticker on each exposed face of each unit cube.
How many stickers from the pack are left?
Show answer & extension
Hide answer & extension
\(2009=7\times 7\times 41\), so there are four possible sets of dimensions of the cuboid:
$$1\times 1\times 2009$$
$$1\times 7\times 287$$
$$1\times 41\times 49$$
$$7\times 7\times 41$$
In the first three cuboids, there is a face with an area of 2009 units (\(2009\times 1\), \(7\times 287\) and \(41\times 49\) respectively) and so 2009 stickers will not be enough. Therefore the cuboid has dimensions \(7\times 7\times 41\) and a surface area of 1246, leaving 763 stickers left over
Extension
For which numbers \(n\) can a cuboid be made with \(n\) unit cube such that \(n\) unit square stickers can cover the faces of the cuboid?
![](javascript:showlimage("ad2022-1ans.png"))