Puzzles
13 December
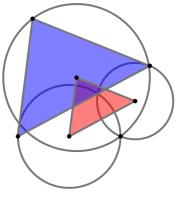
The diagram to the left shows three circles and two triangles. The three circles all meet at one point.
The vertices of the smaller red triangle are at the centres of the circles. The lines connecting the
vertices of the larger blue triangle to the point where all three circles meet are diameters of the
three circles.
The area of the smaller red triangle is 226. What is the area of the larger blue triangle?
Show answer
Hide answer
The two triangles are similar, and the sides of the blue triangle are twice the length of the red triangle. Therefore the area of the blue triangle
is 4 times the area of the red triangle. 226×4=904.
2 December
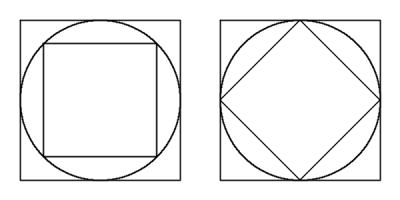
Carol draws a square with area 62. She then draws the smallest possible circle that this square is contained inside.
Next, she draws the smallest possible square that her circle is contained inside. What is the area of her second square?
Show answer
Hide answer
By drawing an appropriate diagram, it can be seen that the small square has half the area of the large square.
Therefore the area of the large square is 124.
19 December
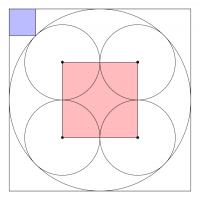
The diagram below shows three squares and five circles.
The four smaller circles are all the same size, and the red square's vertices are the centres of these circles.
The area of the blue square is 14 units. What is the area of the red square?
Show answer
Hide answer
The diagonal of the blue square is \(\sqrt{28}\). The radius \(R\) of the large circle satisfies \(R^2+R^2=(R+\sqrt{28})^2\).
Solving this, we find that \(R=\frac{\sqrt{28}}{\sqrt2-1}=\sqrt{28}(\sqrt2+1)\).
The radius \(r\) of the small circles satisfies \(r+r\sqrt2=R\), and so \(r=\frac{\sqrt{28}(\sqrt2+1)}{\sqrt2+1}=\sqrt{28}\).
The area of the square is \(4r^2=4\left(\sqrt{28}\right)^2=4\times28\). This is 112.
5 December
28 points are spaced equally around the circumference of a circle. There are 3276 ways to pick three of these points.
The three picked points can be connected to form a triangle. Today's number is the number of these triangles that are isosceles.
Show answer
Hide answer
Pick one of the 28 points and imagine a line to the point opposite it. There will be 13 points on each side of this line. Picking one of these 13 points and then picking the
corresponding point on the other side of the line gives an isosceles triangle. Therefore there are 13 isosceles triangles with the first chosen point as the point where the two equal sides meet.
There were 28 choices for the first point, and so the total number of isosceles triangles will be 13×28=364.
2 December
Today's number is the area of the largest dodecagon that it's possible to fit inside a circle with area \(\displaystyle\frac{172\pi}3\).
Two semicircles
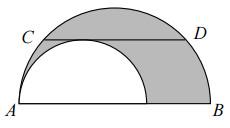
The diagram shows two semicircles.
\(CD\) is a chord of the larger circle and is parallel to \(AB\). The length of \(CD\) is 8m. What is the area of the shaded region (in terms of \(\pi\))?
Show answer & extension
Hide answer & extension
The question does not fix the length of \(AB\), yet implies that there is a unique answer. Therefore we can take \(AB\) to be any length we like and expect the right answer. If \(AB\) is 8m long, then the unshaded semicircle has no area. Therefore the shaded area is \(\tfrac12\pi\times4^2=8\pi\)m.
Extension
How would you calculate the area if you don't assume that the length of \(AB\) doesn't affect the area?
1 December
What is area of the largest area rectangle which will fit in a circle of radius 10?
Show answer
Hide answer
The largest rectangle will be a square. 20 (double the radius) will be the length of its diagonal.
By Pythagoras' Theorem, the sides of the square are \(10\sqrt{2}\). Therefore the area of the square is 200.
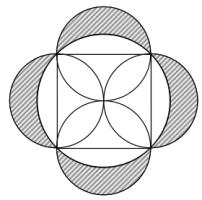
Squared circle
Each side of a square has a circle drawn on it as diameter. The square is also inscribed in a fifth circle as shown.
Find the ratio of the total area of the shaded crescents to the area
of the square.
Show answer
Hide answer
Let the radius of the small circles be \(r\). The are of half of one of these circles is \(\frac{1}{2}\pi r^2\).
The side of the square is \(2r\) and so the area of the square is \(4r^2\). Therefore the area of the whole shape is \((4+2\pi)r^2\).
By Pythagoras' Theorem, the radius of the large circle is \(r\sqrt{2}\). Therefore the area of the circle is \(2\pi r^2\). This means that the shaded area is \((4+2\pi)r^2 - 2\pi r^2\) or \(4r^2\).
This is the same as the area of the square, so the ratio is 1:1.
![](javascript:showlimage("advent2021-circles.png"))
![](javascript:showlimage("ad2020-ans-1.png"))
![](javascript:showlimage("advent2019circles.png"))
![](javascript:showlimage("two-semicircles.jpg"))
![](javascript:showlimage("circles-and-squares.png"))