Sunday Afternoon Maths XVIII
Seven digits
"I'm thinking of a number. I've squared it. I've squared the square. And I've multiplied the second square by the original number. So I now have a number of seven digits whose final digit is a 7," said Dr. Dingo to his daughter.
Can you work out Dr. Dingo's number?
Show answer & extension
Hide answer & extension
Let's call Dr. Dingo's number \(n\). If the number is squared twice then multiplied by \(n\), we get \(n^5\).
For all integers \(n\), the final digit of \(n^5\) is the same as the final digit of \(n\). In other words:
$$n^5\equiv n \mod 10$$
Therefore, the final digit of Dr. Dingo's number is 7.
$$7^5=16807$$
$$17^5=1419857$$
$$27^5=14348907$$
So, in order for the answer to have seven digits, Dr. Dingo's number was 17.
Extension
For which integers \(m\) does there exist an integer \(n\) such that for all integers \(x\):
$$x^n\equiv x \mod m$$
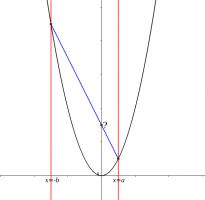
Parabola
On a graph of \(y=x^2\), two lines are drawn at \(x=a\) and \(x=-b\) (for \(a,b>0\). The points where these lines intersect the parabola are connected.
What is the y-coordinate of the point where this line intersects the y-axis?
Show answer & extension
Hide answer & extension
The co-ordinates of the points where the lines intersect the parabola are \((a,a^2)\) and \((-b,b^2)\). Hence the gradient of the line between them is:
$$\frac{a^2-b^2}{a-(-b)}=\frac{(a+b)(a-b)}{a+b}=a-b$$
Therefore the y-coordinate is:
$$b^2 + b(a-b) = ba$$
Ferdinand Möbius, who discovered this property called the curve a Multiplicationsmaschine or 'multiplication machine' as it could be used to perform multiplication.
Extension
How could you use the graph of \(y=x^2\) to divide 100 by 7?
![](javascript:showlimage("parabola.png"))