Sunday Afternoon Maths VIII
Rebounds
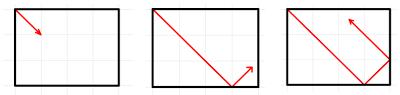
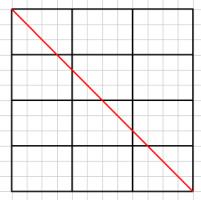
In a 4x3 rectangle, a ball is fired from the top left corner at 45°.
It bounces around a rectangle until it hits a corner. Which corner does it end in?
Which corner will it end in for rectangles of other sizes?
Show answer & extension
Hide answer & extension
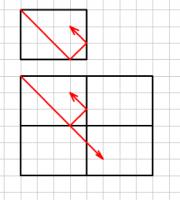
If mirrors were placed along the walls of the rectangle, the ball would appear to travel in a straight line across a grid of rectangles:
Viewed this way, the ball will still stop once it reaches a corner:
For an \(n\) by \(m\) (in above example: \(n=4\), \(m=3\)) rectangle, this will occur once the ball has travelled through \(\mathrm{lcm}(n,m)\) squares.
$$\mathrm{Let\ }a=\frac{\mathrm{lcm}(n,m)}{n}$$
$$\mathrm{Let\ }b=\frac{\mathrm{lcm}(n,m)}{m}$$
On its way to the corner, the ball will bounce \(b-1\) times off the top and bottom and \(a-1\) times off the sides. It can be seen that if \(a-1\) is even, then the ball will end in one of the corners on the right hand side. The complete results can be seen in the following
Carroll diagram:
| \(a-1\) odd | \(a-1\) even |
| \(b-1\) odd | Top left | Top right |
| \(b-1\) even | Bottom left | Bottom right |
It can be shown that the ball will never finish in the top left (where it started) as this would require it to travel through the bottom right first. Therefore the following holds:
| \(a\) even | \(a\) odd |
| \(b\) even | | Top right |
| \(b\) odd | Bottom left | Bottom right |
Extension
For which sizes of rectangle will the path of the ball make the same pattern?
Complex squares
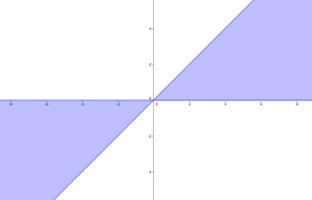
For which complex numbers, \(z\), are \(\mathrm{Re}(z^2)\) and \(\mathrm{Im}(z^2)\) both positive?
Show answer & extension
Hide answer & extension
Any complex number can be written in the form \(z=re^{i\theta}\).
This gives that \(z^2=r^2e^{2i\theta}\), which will have positive real and complex parts when \(0+2\pi n < 2\theta < \frac{\pi}{2}+2\pi n\).
This will occur when \(0 < \theta < \frac{\pi}{4}\) and \(\pi < \theta < \frac{5\pi}{4}\).
A complex number \(z\) falls in these regions when \(|\mathrm{Re}(z)|>|\mathrm{Im}(z)|\) and \(\mathrm{sign}(\mathrm{Re}(z))=\mathrm{sign}(\mathrm{Im}(z))\).
Extension
For which complex numbers, \(z\), are \(\mathrm{Re}(z^3)\) and \(\mathrm{Re}(z^3)\) both positive?
Adding bases
Let \(a_b\) denote \(a\) in base \(b\).
Find bases \(A\), \(B\) and \(C\) less than 10 such that \(12_A+34_B=56_C\).
Reverse bases again
Find three digits \(a\), \(b\) and \(c\) such that \(abc\) in base 10 is equal to \(cba\) in base 9?
Show answer & extension
Hide answer & extension
445 in base 10 is equal to 544 in base 7.
Extension
Find another pair of bases \(A\) and \(B\) so that there exist digits \(d\), \(e\) and \(f\) such that \(def\) in base \(A\) is equal to \(fed\) in base \(B\)?
Two
Find \(a\) such that \(a+(a+A)^{-1}=2\), where \(A=(a+A)^{-1}\).
ie. \(a + \frac{1}{a + \frac{1}{a + \frac{1}{a + \frac{1}{...}}}} = 2\).
Find \(b\) such that \(b+(b+B)^{\frac{1}{2}}=2\), where \(B=(b+B)^{\frac{1}{2}}\).
ie. \(b + \sqrt{b + \sqrt{b + \sqrt{b + \sqrt{...}}}} = 2\).
Find \(c\) such that \(c+(c+C)^{2}=2\), where \(C=(c+C)^{2}\).
In terms of \(k\), find \(d\) such that \(d+(d+D)^{k}=2\), where \(D=(d+D)^{k}\).