Sunday Afternoon Maths LXIII
Posted on 2018-04-22
Is it equilateral?
Source: Chalkdust issue 07
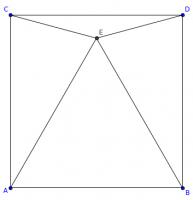
In the diagram below, \(ABDC\) is a square. Angles \(ACE\) and \(BDE\) are both 75°.
Is triangle \(ABE\) equilateral? Why/why not?
Cube multiples
Source: Radio 4's Puzzle for Today (set by Daniel Griller)
Six different (strictly) positive integers are written on the faces of a cube. The sum of the numbers on any two adjacent faces is a multiple of 6.
What is the smallest possible sum of the six numbers?
If you enjoyed these puzzles, check out Advent calendar 2023,
puzzles about combinatorics, or a random puzzle.
puzzles about combinatorics, or a random puzzle.