Hide answer & extension
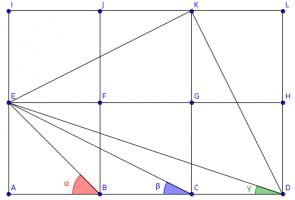
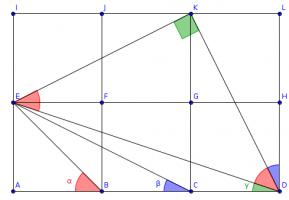
Draw three more squares and add these lines (I have coloured the angles to make equal angles clearer):
Triangles \(ACE\), \(LDK\) and \(IKE\) are congruent, so angle \(KDL\) is equal to \(\beta\).
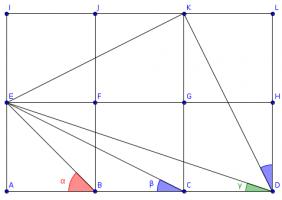
The congruence of these triangles tells us that angles \(DKL\) and \(EKI\) add up to a right angle, so angle \(EKD\) is also a right angle.
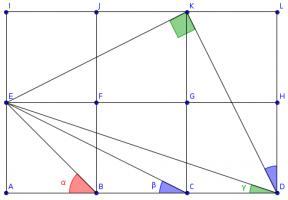
The congruence of the triangles also tells us that \(KD\) and \(KE\) are the same length and so angle \(EDK\) is the angle in an isosceles right-angled triangle. \(\alpha\) is also the angle in an isosceles right-angled triangle, so these two angles are equal.
Therefore \(\alpha+\beta+\gamma=90^\circ\).
Extension
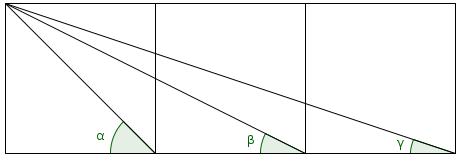
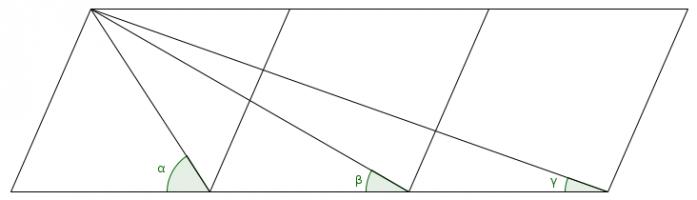
The diagram shows three rhombuses with diagonals drawn on and three angles labelled.
What is the value of \(\alpha+\beta+\gamma\)?
![](javascript:showlimage("three-squares.png"))
![](javascript:showlimage("three-ans1.png"))
![](javascript:showlimage("three-ans2.png"))
![](javascript:showlimage("three-ans3.png"))
![](javascript:showlimage("three-ans4.png"))
![](javascript:showlimage("three-rhombus.png"))