Hide answer & extension
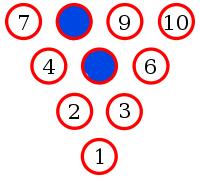
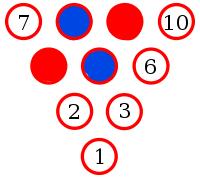
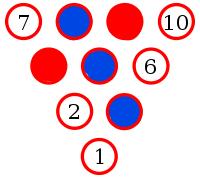
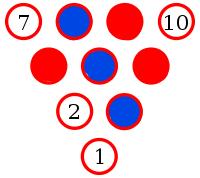
Yes. To show this, let's suppose there is an arrangement of pins with no monochrome triangle.
Let the middle pin be blue (if it is not blue, then swapping all the colours will make it blue without adding/removing monochrome triangles).
Pins 8, 2 and 6 make a triangle. Therefore one of these pins must be blue. By symmetry, any of these situations is equivalent to 8 being blue.
Pins 9 and 4 must be red to prevent a blue triangle.
Pin 3 must be blue to prevent a red triangle.
Pin 6 must be red to prevent a blue triangle.
But now whichever colour 10 is, it will make a monochrome triangle. Therefore there must be three pins of the same colour which lie on the vertices of an equilateral triangle.
Extension
What is the smallest \(n\) such that any mixture of \(n^2\) red and blue pins arranged in a square grid must contain four pins of the same colour which lie on the vertices of a square?
![](javascript:showlimage("bowling-pins.png"))
![](javascript:showlimage("bowling-a1.png"))
![](javascript:showlimage("bowling-a2.png"))
![](javascript:showlimage("bowling-a3.png"))
![](javascript:showlimage("bowling-a4.png"))
![](javascript:showlimage("bowling-a5.png"))