Puzzles
Cutting corners
Source: New Scientist Enigma 1773
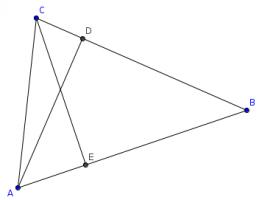
The diagram below shows a triangle \(ABC\). The line \(CE\) is perpendicular to \(AB\) and the line \(AD\) is perpedicular to \(BC\).
The side \(AC\) is 6.5cm long and the lines \(CE\) and \(AD\) are 5.6cm and 6.0cm respectively.
How long are the other two sides of the triangle?
If you enjoyed this puzzle, check out Sunday Afternoon Maths VLIII,
puzzles about triangles, or a random puzzle.
puzzles about triangles, or a random puzzle.