Puzzles
Polygraph
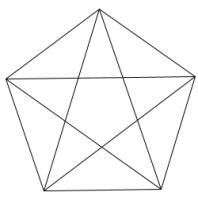
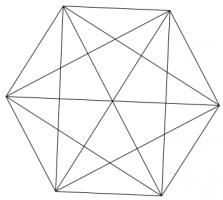
Draw a regular polygon. Connect all its vertices to every other vertex. For example, if you picked a pentagon or a hexagon, the result would look as follows:
![](javascript:showlimage("polygraph2.png"))
![](javascript:showlimage("polygraph1.png"))
Colour the regions of your shape so that no two regions which share an edge are the same colour. (Regions which only meet at one point can be the same colour.)
What is the least number of colours which this can be done with?
If you enjoyed this puzzle, check out Sunday Afternoon Maths XLI,
puzzles about regular shapes, or a random puzzle.
puzzles about regular shapes, or a random puzzle.