Blog
2016-12-23
In many early arcade games, the size of the playable area was limited by the size of the screen. To make this area seem larger, or to
make gameplay more interesting, many games used wraparound; allowing the player to leave one side of the screen and return on another.
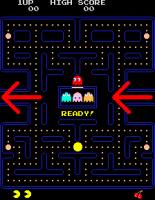
In Pac-Man, for example, the player could leave the left of the screen along the arrow shown and return
on the right, or vice versa.
![](javascript:showlimage("pac-arrows.png"))
Pac-Man's apparent teleportation from one side of the screen to the other may seem like magic, but it is more easily explained by
the shape of Pac-Man's world being a cylinder.
![](javascript:showlimage("pac-cylinder.png"))
Rather than jumping or teleporting from one side to the other, Pac-Man simply travels round the cylinder.
Bubble Bobble was first released in 1986 and features two dragons, Bub and Bob, who are tasked with
rescuing their girlfriends by trapping 100 levels
worth of monsters inside bubbles. In these levels, the dragons and monsters may leave the bottom of the screen to return at the top.
Just like in Pac-Man, Bub and Bob live on the surface of a cylinder, but this time it's horizontal not vertical.
![](javascript:showlimage("bubbob-flat.png"))
![](javascript:showlimage("bubbob-cylinder.png"))
A very large number of arcade games use left-right or top-bottom wrapping and have the same cylindrical shape as Pac-Man or Bubble Bobble.
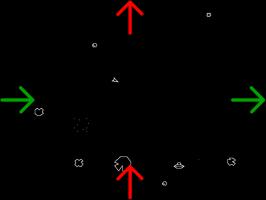
In Asteroids, both left-right and top-bottom wrapping are used.
![](javascript:showlimage("asteroids-arrows.png"))
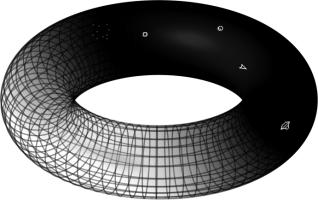
The ships and asteroids in Asteroids live on the surface of a torus, or doughnut: a cylinder around to make its two ends meet up.
![](javascript:showlimage("asteroids-torus.png"))
There is, however, a problem with the torus show here. In Asteroids, the ship will take amount of time to get from the left of the screen
to the right however high or low on the screen it is. But the ship can get around the inside of the torus shown faster than it can
around the outside, as the inside is shorter. This is because the screen of play is completely flat, while the inside and outside halves of
the torus are curved.
It is impossible to make a flat torus in three-dimensional space, but it is possible to make one in
four-dimensional space.
Therefore, while Asteroids seems to be a simple two-dimensional game, it is actually taking place on a four-dimensional surface.
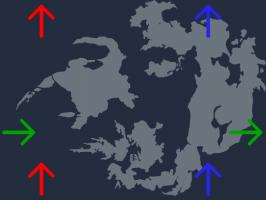
Wrapping doesn't only appear in arcade games. Many games in the excellent Final Fantasy series use wrapping on the world maps, as shown here
on the Final Fantasy VIII map.
![](javascript:showlimage("ff8-arrows.png"))
Just like in Asteroids, this wrapping means that Squall & co. carry out their adventure on the surface of a four-dimensional flat torus.
The game designers, however, seem to not have realised this, as shown in this screenshot including a spherical (!) map.
![](javascript:showlimage("ff8-sphere.png"))
Due to the curvature of a sphere, lines that start off parallel eventually meet. This makes it impossible to map
nicely between a flat surface to a sphere (this is why so many different map projections exist), and heavily complicates the task of making
a game with a truly spherical map. So I'll let the Final Fantasy VIII game designers off. Especially since the rest of the game is such
incredible fun.
It is sad, however, that there are no games (at leat that I know of) that make use of the great variety of different wrapping rules available. By only
slightly adjusting the wrapping rules used in the games in this post, it is possible to make games on a variety of other surfaces,
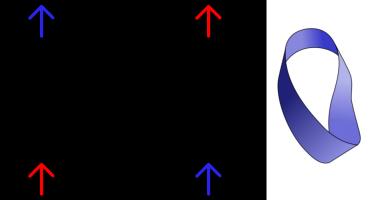
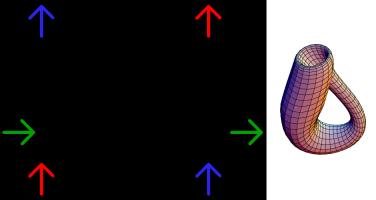
such a Klein bottles or Möbius strips as shown below.
![](javascript:showlimage("mobius-video-game.png"))
![](javascript:showlimage("klein-video-game.png"))
If you know of any games make use of these surfaces, let me know in the comments below!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
⭐ top comment (2022-05-28) ⭐
Thanks for postOliver
×1 HyperRogue also has special modes which experiment with other geometries (spherical, and elliptic which is non-orientable). Hydra Slayer has Mobius strip and Klein bottle levels.
Zeno Rogue
HyperRogue is an example of a game that takes place on the hyperbolic plane. Rather than looping, the map is infinite.
See: http://zenorogue.blogspot.com.au/2012/...
See: http://zenorogue.blogspot.com.au/2012/...
maetl
Hyperrogue may be the only game in existence with a hyperbolic surface topology: http://www.roguetemple.com/z/hyper/
zaratustra
F-Zero GX had a track called Mobius Ring, that was... well, a Möbius ring.
F-Zero X had a more trivial track that was just the outward side of a regular ring, but it was rather weird too, because it meant that this was a looping track that had no turns.
F-Zero X had a more trivial track that was just the outward side of a regular ring, but it was rather weird too, because it meant that this was a looping track that had no turns.
Olaf
Add a Comment
2016-03-31
Pythagoras's Theorem is perhaps the most famous theorem in maths. It is also very old, and for over 2500 years mathematicians have been explaining why it is true.
This has led to hundreds of different proofs of the theorem. Many of them were collected in the 1920s in The pythagorean proposition by Elisha Scott Loomis [1]. Let's have a look at some of them.
Using similar triangles
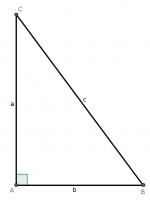
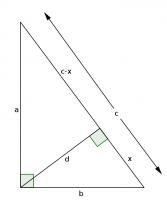
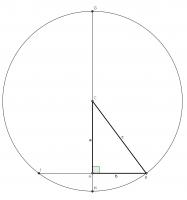
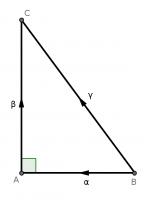
For our first proof, start with a right angled triangle, \(ABC\), with sides of lengths \(a\), \(b\) and \(c\).
![](javascript:showlimage("pyth0.png"))
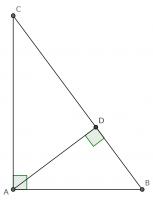
Add a point \(D\) on the hypotenuse such that the line \(AD\) is perpendicular to \(BC\). Name the lengths as shown in the second diagram.
![](javascript:showlimage("pyth1.png"))
![](javascript:showlimage("pyth2.png"))
\(ABC\) and \(DBA\) are similar triangles, so:
$$\frac{b}{x}=\frac{c}{b}$$
$$b^2=xc$$
\(ABC\) and \(DAC\) are similar triangles, so:
$$\frac{a}{c-x}=\frac{c}{a}$$
$$a^2=c^2-cx$$
Adding the two equations gives:
$$a^2+b^2=c^2$$
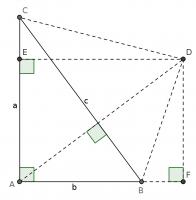
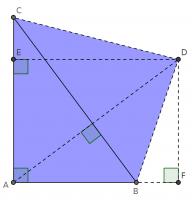
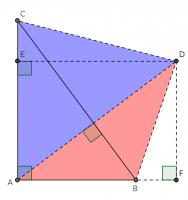
Constructing a quadrilateral
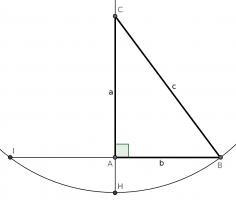
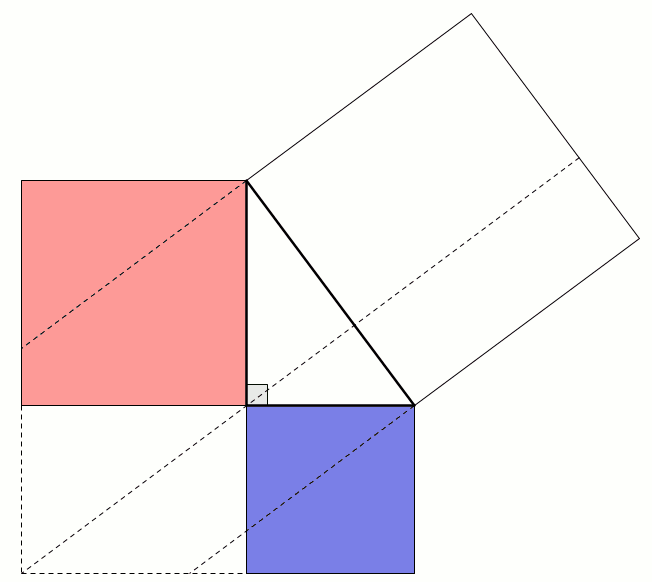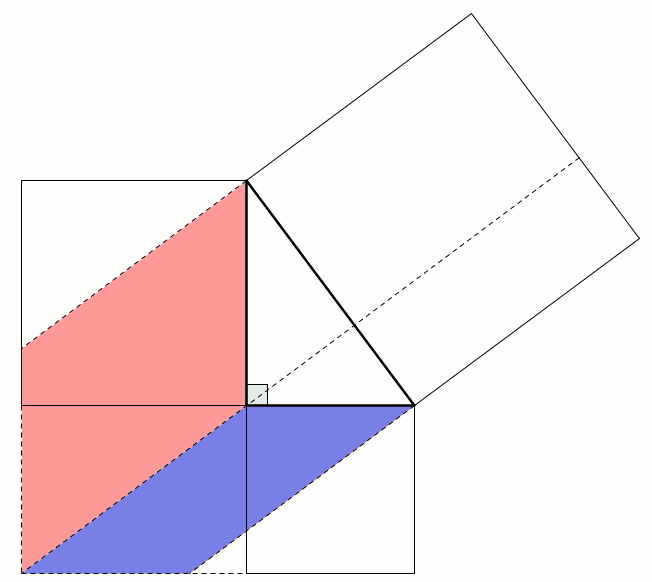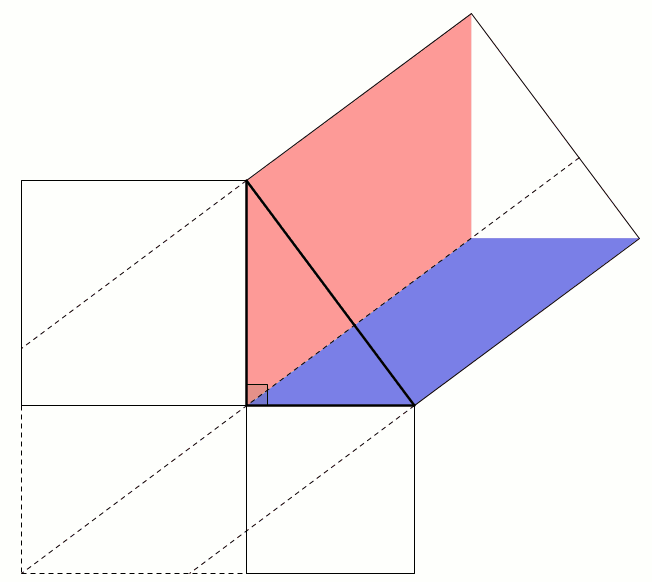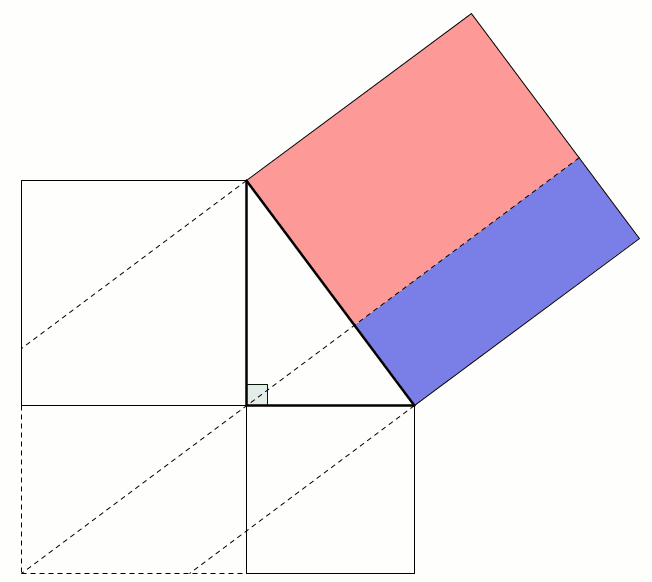
This proof shows the theorem is true by using extra lines and points added to the triangle. Start with \(ABC\) as before then add a point \(D\) such that \(AD\) and \(BC\) are perpendicular and of equal length. Add points \(E\) on \(AC\) and \(F\) on \(AB\) (extended) such that \(DE\) and \(AC\) are perpendicular and \(DF\) and \(AB\) are perpendicular.
![](javascript:showlimage("pyth3.png"))
By similar triangles, it can be seen that \(DF=b\) and \(DE=a\).
As the two diagonals of \(BACD\) are perpendicular, its area is \(\tfrac12c^2\).
![](javascript:showlimage("pyth4.png"))
The quadrilateral \(BACD\).
The area of \(BACD\) is also equal to the sum of the areas of \(ABD\) and \(ACD\). The area of \(ABD\) is \(\tfrac12b^2\). The area of \(ACD\) is \(\tfrac12a^2\).
![](javascript:showlimage("pyth5.png"))
The triangles \(ABD\) and \(ACD\).
Therefore, \(\tfrac12a^2+\tfrac12b^2=\tfrac12c^2\), which implies that \(a^2+b^2=c^2\).
Using a circle
This proof again uses extra stuff: this time using a circle. Draw a circle of radius \(c\) centred at \(C\). Extend \(AC\) to \(G\) and \(H\) and extend \(AB\) to \(I\).
![](javascript:showlimage("pyth6.png"))
![](javascript:showlimage("pyth6-zoomed.png"))
By the intersecting chord theorem, \(AH\times AG = AB\times AI\). Using the facts that \(AI=AB\) and \(CH\) and \(CG\) are radii, the following can be obtained from this:
$$(c-a)\times(c+a)=b\times b$$
$$c^2-a^2=b^2$$
$$a^2+b^2=c^2$$
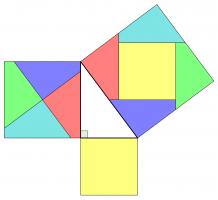
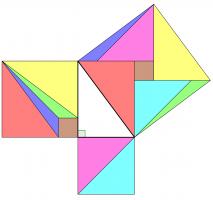
Rearrangement proofs
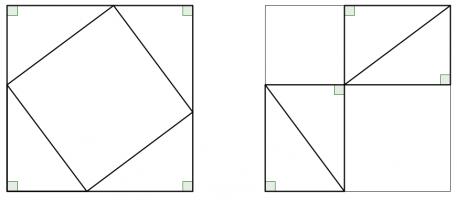
A popular method of proof is dissecting the smaller squares and rearranging the pieces to make the larger square. In both the following, the pieces are coloured to show which are the same:
![](javascript:showlimage("pyth-re1.png"))
![](javascript:showlimage("pyth-re2.png"))
Alternatively, the theorem could be proved by making copies of the triangle and moving them around. This proof was presented in The pythagorean proposition simply with the caption "LOOK":
![](javascript:showlimage("pyth-re3.png"))
Moving proof
This next proof uses the fact that two parallelograms with the same base and height have the same area: sliding the top side horizontally does not change the area. This allows us to move the smaller squares to fill the large square:
![](javascript:showlimage("pyth-moving1-squashed.gif"))
Using vectors
For this proof, start by labelling the sides of the triangle as vectors \(\alpha\), \(\beta\) and \(\gamma\).
![](javascript:showlimage("pyth7.png"))
Clearly, \(\gamma = \alpha+\beta\). Taking the dot product of each side with itself gives:
$$\gamma\cdot\gamma = \alpha\cdot\alpha+2\alpha\cdot\beta+\beta\cdot\beta$$
\(\alpha\) and \(\beta\) are perpendicular, so \(\alpha\cdot\beta=0\); and dotting a vector with itself gives the size of the vector squared, so:
$$|\gamma|^2=|\alpha|^2+|\beta|^2$$
If you don't like any of these proofs, there are of course many, many more. Why don't you tweet me your favourite.
References
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment