Blog
2020-01-02
It's 2020, and the Advent calendar has disappeared, so it's time to reveal the answers and annouce the winners.
But first, some good news: with your help, Santa and his two reindeer were found and Christmas was saved!
Now that the competition is over, the questions and all the answers can be found here.
Before announcing the winners, I'm going to go through some of my favourite puzzles from the calendar, reveal the solution and a couple of notes and Easter eggs.
Highlights
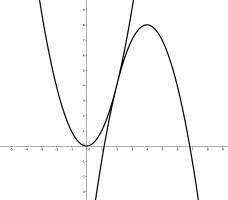
My first highlight is this puzzle from 10 December that seems difficult to get started on, but plotting the two quadratics reveals a very useful piece of information that can be used.
10 December
For all values of \(x\), the function \(f(x)=ax+b\) satisfies
$$8x-8-x^2\leqslant f(x)\leqslant x^2.$$
What is \(f(65)\)?
Edit: The left-hand quadratic originally said \(8-8x-x^2\). This was a typo and has now been corrected.
My next highlight is the puzzle from 12 December, which was election day in the UK. Although the puzzle isn't that difficult or interesting to calculate, the answer is surprising enough
to make this one of my favourites.
12 December
For a general election, the Advent isles are split into 650 constituencies. In each constituency, exactly 99 people vote: everyone votes for one of the two main parties: the Rum party or the
Land party. The party that receives the most votes in each constituency gets an MAP (Member of Advent Parliament) elected to parliament to represent that constituency.
In this year's election, exactly half of the 64350 total voters voted for the Rum party. What is the largest number of MAPs that the Rum party could have?
My next highlight is the puzzle from 13 December. If you enjoyed this one, then you can find a puzzle based on a similar idea on the puzzles
pages of issue 10 of Chalkdust.
13 December
Each clue in this crossnumber (except 5A) gives a property of that answer that is true of no other answer. For example: 7A is a multiple of 13; but 1A, 3A, 5A, 1D, 2D, 4D, and 6D are all not multiples of 13.
No number starts with 0.
|
| ||||||||||||||||||||||||||||||||||||||||||||||
My final highlight is the puzzle from 16 December. I always include a few of these, as they can be designed to give any answer so are useful for making the final logic puzzle work.
But I was particularly happy with this one.
16 December
Arrange the digits 1-9 in a 3×3 square so that:
the median number in the first row is 6;
the median number in the second row is 3;
the mean of the numbers in the third row is 4;
the mean of the numbers in the second column is 7;
the range of the numbers in the third column is 2,
The 3-digit number in the first column is today's number.
| median 6 | |||
| median 3 | |||
| mean 4 | |||
| today's number | mean 7 | range 2 |
Notes and Easter eggs
A few of you may have noticed the relevance of the colours assigned to each island:
Rum (Red Rum),
Land (Greenland),
Moon (Blue Moon), and
County (Orange County).
Once you've entered 24 answers, the calendar checks these and tells you how many are correct. I logged the answers that were sent
for checking and have looked at these to see which puzzles were the most and least commonly incorrect. The bar chart below shows the total number
of incorrect attempts at each question.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Day | |||||||||||||||||||||||
You can see that the most difficult puzzles were those on
4 and
15 December;
and the easiest puzzles were on
3,
11,
17, and
24 December.
This year, the final logic puzzle revealed the positions of Santa, Rudolph and Blitzen, then you had to find them on this map.
The map has 6 levels, with 81 positions on each level, so the total size of the map is \(81^6=282\,429\,536\,481\) squares.
This is a lot; one Advent solver even wondered how large a cross stitch of the whole thing would be.
I obviously didn't draw 282 billion tiles: the whole map was generated using the following tiles, which were reused across the map.

The map tiles.
I also snuck a small Easter egg into the map. Below the Advent calendar, this example was shown:
If you actually visited this position on the map, you found Wally.
At least one Advent solver appears to have found Wally, as they left this cryptic comment under the name Dr Matrix
(an excellent Martin Gardner reference).
The solution
The solutions to all the individual puzzles can be found here.
Using the daily clues, it was possible to work out that
Santa was at 36.11.19.79.79.43, Blitzen was at 23.12.23.11.23.11, and Rudolph was at 16.64.16.16.16.64.
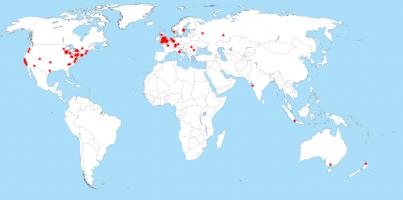
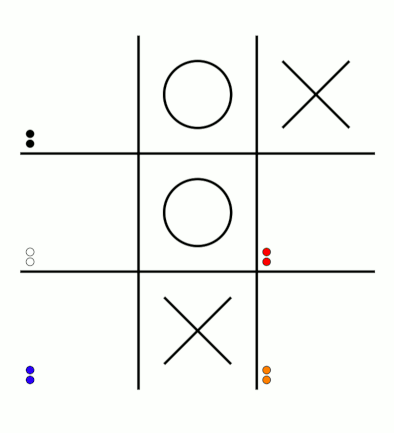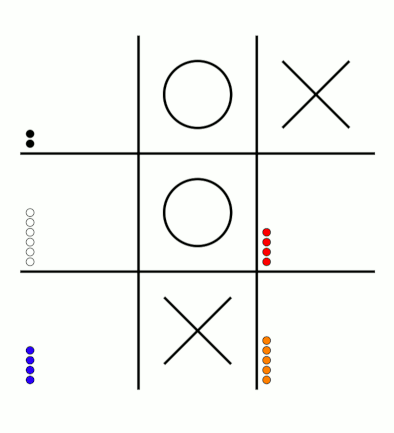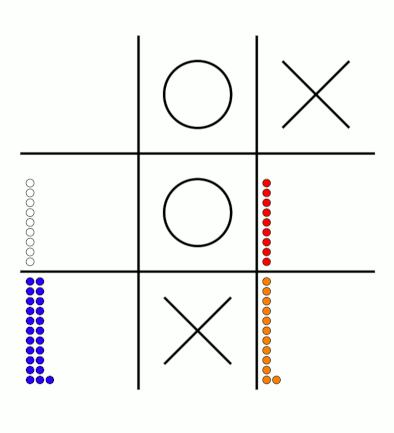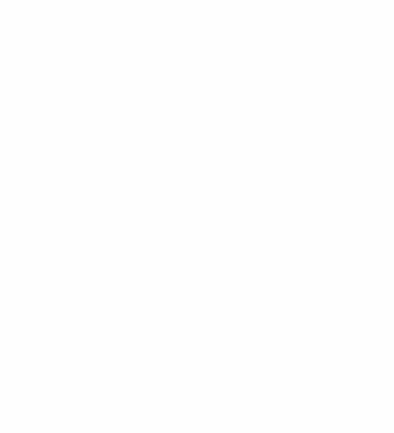
And finally (and maybe most importantly), on to the winners: 126 people found Santa and both reindeer and entered the competition. Their (very) approximate locations are shown on this map:
From the correct answers, the following 10 winners were selected:
| 1 | Valentin Valciu |
| 2 | Tom Anderson |
| 3 | Alex Bolton |
| 4 | Kevin Fray |
| 5 | Jack Kiuttu |
| 6 | Ben Baker |
| 7 | Joe Gage |
| 8 | Michael Thomas |
| 9 | Martin Holtham |
| 10 | Beth Jensen |
Congratulations! Your prizes will be on their way shortly.
The prizes this year include 2019 Advent calendar T-shirts. If you didn't win one, but would like one of these, you can buy one at mscroggs.co.uk/tshirt until 7 January
(when I will be sending them for printing).
Additionally, well done to
Adam Abrams, Adam NH, Adam Vellender, Alan Buck, Alex Ayres, Alex Burlton, Alexander Ignatenkov, Andrew Ennaco, Andrew Tindall, Artie Smith, Ashley Jarvis, Austin Antoniou, Becky Russell,
Ben Jones, Ben Reiniger, Brennan Dolson, Brian Carnes, Carl Westerlund, Carmen Guenther, Clare Wallace, Colin Beveridge, Connie, Corbin Groothuis, Cory Peters, Dan Colestock, Dan DiMillo,
Dan Whitman, David, David Ault, David Fox, Diane Keimel, Duncan Ramage, Emilie Heidenreich, Emily Troyer, Eric, Eric Kolbusz, Erik Eklund, Evan Louis Robinson, Frances Haigh, Franklin Ta,
Fred Verheul, Félix Breton, Gabriella Pinter, Gautam Webb, Gert-Jan de Vries, Hart Andrin, Heerpal Sahota, Herschel Pecker, Jacob Juillerat, Jan, Jean-Noël Monette, Jen Shackley,
Jeremiah Southwick, Jessica Marsh, Johan Asplund, John Warwicker, Jon Foster, Jon Palin, Jonathan Chaffer, Jonathan Winfield, Jose, Kai, Karen Climis, Karen Kendel, Katja Labermeyer, Laura,
Lewis Dyer, Louis de Mendonca, M Oostrom, Magnus Eklund, Mahmood Hikmet, Marian Clegg, Mark Stambaugh, Martin Harris, Martine Vijn Nome, Matt Hutton, Matthew Askins, Matthew Schulz,
Maximilian Pfister, Melissa Lucas, Mels, Michael DeLyser, Michael Gustin, Michael Horst, Michael Prescott, Mihai Zsisku, Mike, Mikko, Moreno Gennari, Nadine Chaurand, Naomi Bowler, Nathan C,
Pat Ashforth, Paul Livesey, Pranshu Gaba, Raymond Arndorfer, Riccardo Lani, Rosie Paterson, Rupinder Matharu, Russ Collins, S A Paget, SShaikh, Sam Butler, Sam Hartburn, Scott, Seth Cohen,
Shivanshi Adlakha, Simon Schneider, Stephen Cappella, Stephen Dainty, Steve Blay, Thomas Tu, Tom Anderson, Tony Mann, Yasha, and Yuliya Nesterova,
who all also submitted the correct answer but were too unlucky to win prizes this time.
See you all next December, when the Advent calendar will return.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Never mind, I found them, they were your example ASC. Very clever!
Michael T
Where did the coordinates for Wally come from? Are they meaningful, or are they just some random coordinates thrown together?
Michael T
Add a Comment
2019-12-27
In tonight's Royal Institution Christmas lecture,
Hannah Fry and Matt Parker demonstrated how machine learning works using MENACE.
The copy of MENACE that appeared in the lecture was build and trained by me. During the training, I logged all the moved made by MENACE and the humans playing against them, and using this data I have
created some visualisations of the machine's learning.
First up, here's a visualisation of the likelihood of MENACE choosing different moves as they play games. The thickness of each arrow represented the number of beads in the box corresponding to that move,
so thicker arrows represent more likely moves.
The likelihood that MENACE will play each move.
There's an awful lot of arrows in this diagram, so it's clearer if we just visualise a few boxes. This animation shows how the number of beads in the first box changes over time.
You can see that MENACE learnt that they should always play in the centre first, an ends up with a large number of green beads and almost none of the other colours. The following
animations show the number of beads changing in some other boxes.
MENACE learns that the top left is a good move.
MENACE learns that the middle right is a good move.
MENACE is very likely to draw from this position so learns that almost all the possible moves are good moves.
The numbers in these change less often, as they are not used in every game: they are only used when the game reached the positions shown on the boxes.
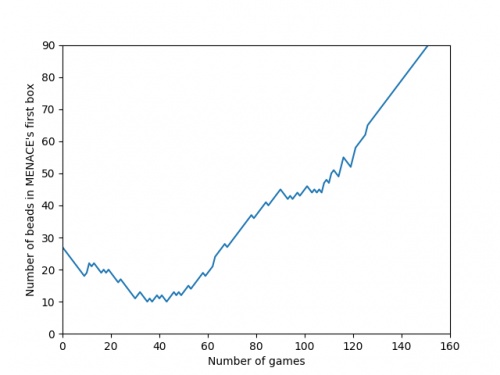
We can visualise MENACE's learning progress by plotting how the number of beads in the first box changes over time.
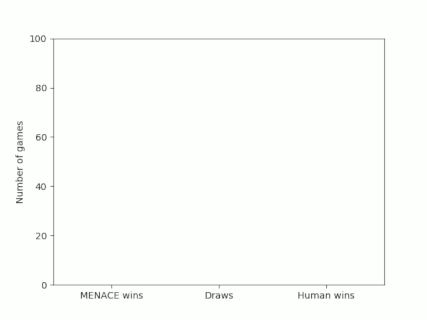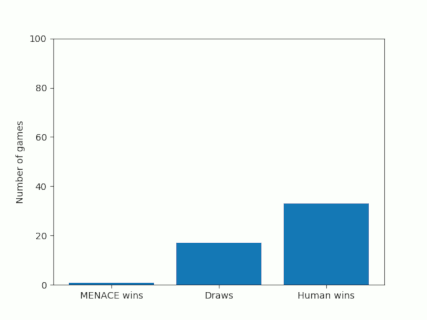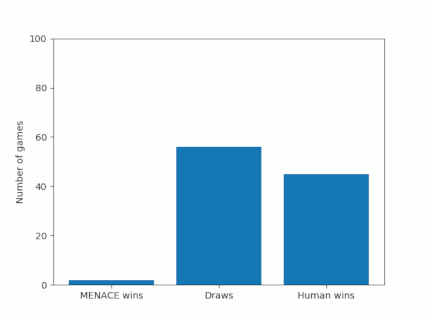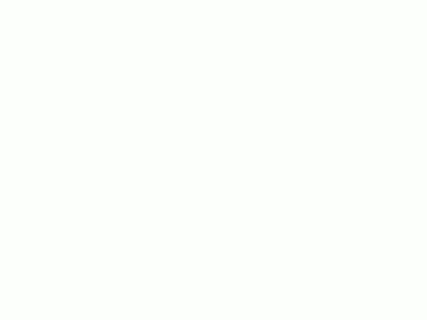
Alternatively, we could plot how the number of wins, loses and draws changes over time or view this as an animated bar chart.
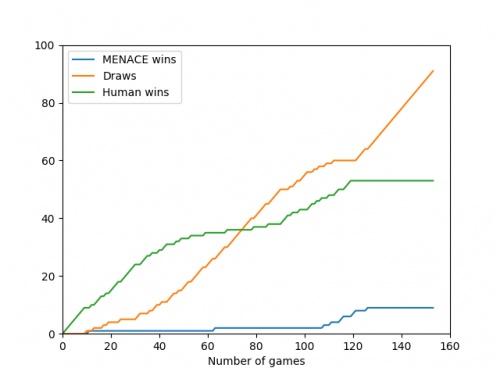
The number of games MENACE wins, loses and draws.
The number of games MENACE has won, lost and drawn.
If you have any ideas for other interesting ways to present this data, let me know in the comments below.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@(anonymous): Have you been refreshing the page? Every time you refresh it resets MENACE to before it has learnt anything.
It takes around 80 games for MENACE to learn against the perfect AI. So it could be you've not left it playing for long enough? (Try turning the speed up to watch MENACE get better.)
It takes around 80 games for MENACE to learn against the perfect AI. So it could be you've not left it playing for long enough? (Try turning the speed up to watch MENACE get better.)
Matthew
I have played around menace a bit and frankly it doesnt seem to be learning i occasionally play with it and it draws but againt the perfect ai you dont see as many draws, the perfect ai wins alot more
(anonymous)
@Colin: You can set MENACE playing against MENACE2 (MENACE that plays second) on the interactive MENACE. MENACE2's starting numbers of beads and incentives may need some tweaking to give it a chance though; I've been meaning to look into this in more detail at some point...
Matthew
Idle pondering (and something you may have covered elsewhere): what's the evolution as MENACE plays against itself? (Assuming MENACE can play both sides.)
Colin
Add a Comment
2019-12-08
Just like last year, the year before and the year before, TD and I spent some time in November this year designing a Chalkdust puzzle Christmas card.
The card looks boring at first glance, but contains 9 puzzles. By splitting the answers into two digit numbers, then drawing lines labelled with each number (eg if an answer is 201304, draw the lines labelled 20, 13 and 4), you will reveal a Christmas themed picture. Colouring the regions of the card containing circles red, the regions containing squares green, and the regions containing stars white or yellow will make this picture even nicer.
If you want to try the card yourself, you can download this pdf. Alternatively, you can find the puzzles below and type the answers in the boxes. The answers will be automatically be split into two digit numbers, the lines will be drawn, and the regions will be coloured...
| 1. | If you write out the numbers from 1 to 10,000 (inclusive), how many times will you write the digit 1? | Answer |
| 2. | What is the sum of all the odd numbers between 0 and 86? | Answer |
| 3. | How many numbers between 1 and 4,008,004 (inclusive) have an odd number of factors (including 1 and the number itself)? | Answer |
| 4. | In a book with pages numbered from 1 to 130,404, what do the two page numbers on the centre spread add up to? | Answer |
| 5. | What is the area of the largest area quadrilateral that will fit inside a circle with area 60,153π? | Answer |
| 6. | There are 5 ways to write 4 as the sum of ones and twos (1+1+1+1, 1+1+2, 1+2+1, 2+1+1, and 2+2). How many ways can you write 28 as the sum of ones and twos? | Answer |
| 7. | What is the lowest common multiple of 1025 and 835? | Answer |
| 8. | How many zeros does 245! (245!=245×244×243×...×1) end in? | Answer |
| 9. | Carol picked a 6-digit number then removed one of its digits to make a 5-digit number. The sum of her 6-digit and 5-digit numbers is 334877. Which 6-digit number did she pick? | Answer |
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Thanks for the feedback. (I now understand the need for redaction). My son sent me your link as a Xmas present. I must think of an appropriate retaliation. (What is a PDF?)Think I've fixed 1,6 and 9....8 eludes me, for the moment.
Rob
@Rob: It looks to me like you've made mistakes in questions 1, 6, 8, and 9. The hints from the back of the pdf might help:
1. How many numbers between 1 and 10,000 have 1 as their final digit? How many have 1 as their penultimate digit?
6. How many ways can you write 1? 2? 3? 4? 5? What's the pattern?
8. How many zeros does 10! end in? How many zeros does 20! end in? How many zeros does 30! end in?
9. Carol’s sum is odd. What does this tell you about the 5- and 6-digit numbers?
1. How many numbers between 1 and 10,000 have 1 as their final digit? How many have 1 as their penultimate digit?
6. How many ways can you write 1? 2? 3? 4? 5? What's the pattern?
8. How many zeros does 10! end in? How many zeros does 20! end in? How many zeros does 30! end in?
9. Carol’s sum is odd. What does this tell you about the 5- and 6-digit numbers?
Matthew
I'm 71, with one good eye left. What am I missing?
1. 400001
2. 1849
3. 2002
4. 130405
5. 120306
6. 53?
7. 171175
8. 59?
9. 313525
1. 400001
2. 1849
3. 2002
4. 130405
5. 120306
6. 53?
7. 171175
8. 59?
9. 313525
Rob
Add a Comment
2019-11-24
This year, the front page of mscroggs.co.uk will once again feature an Advent calendar, just like
last year, the year before, the year before and the year before. Behind each door, there will be a puzzle with a three digit solution. The solution to each day's puzzle forms part of a logic puzzle:
It's nearly Christmas and something terrible has happened: while out on a test flight, Santa's sled was damaged and Santa, Rudolph and Blitzen fell to the ground over the Advent Isles.
You need to find Santa and his reindeer before Christmas is ruined for everyone.
You have gathered one inhabitant of the four largest Advent Isles—Rum, Land, Moon and County—and they are going to give you a series of clues about where Santa and his reindeer landed.
However, one or more of the islanders you have gathered may have been involved in damaging Santa's sled and causing it to crash: any islander involved in this will lie to you to attempt to stop
you from finding Santa and his reindeer.
Once you are ready to search for Santa, Rudolph and Blitzen, you can find the map by following this link.
Each of the clues will be about Santa's, Rudolph's or Blitzen's positions in Advent Standard Coordinates (ASC): ASC are given by six two-digit numbers with dots inbetween, for example
12.52.12.13.84.55.
For this example coordinate, the islanders will refer to
(the first) 12 as the first coordinate,
52 as the second coordinate,
(the second) 12 as the third coordinate,
13 as the fourth coordinate,
84 as the fifth coordinate, and
55 as the sixth coordinate.
To find a point's ASC coordinates, split a map of the islands into a 9×9 grid, then number the rows and columns 1 to 9: the first two digits of ASC give the vertical then horizontal position of a square in this grid.
The next two digits then give a smaller square when this square is then itself split into a 9×9 grid, and so on. An example is show below.
Behind each day (except Christmas Day), there is a puzzle with a three-digit answer.
Each of these answers forms part of a fact that one of the islanders tells you.
You must use these clues to find Santa and his two reindeer.
Ten randomly selected people who solve all the puzzles, find Santa and his reindeer, and fill in the entry form behind the door on the 25th will win prizes!
The winners will be randomly chosen from all those who submit the entry form before the end of 2019. Each day's puzzle (and the entry form on Christmas Day) will be available from 5:00am GMT. But as the winners will be selected randomly,
there's no need to get up at 5am on Christmas Day to enter!
As you solve the puzzles, your answers will be stored. To share your stored answers between multiple devices, enter your email address below the calendar and you will be emailed a magic link to visit on your other devices.
To win a prize, you must submit your entry before the end of 2019. Only one entry will be accepted per person. If you have any questions, ask them in the comments below or on Twitter.
So once December is here, get solving! Good luck and have a very merry Christmas!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
This search space is so large, it's way harder than trying to find Wally like in the children's books. Best to read everything carefully looking for any clues, and then solve all the puzzles and logic before searching randomly!
Did you know Wally is called Waldo in the US, Walter in Germany, and Charlie in France?
Did you know Wally is called Waldo in the US, Walter in Germany, and Charlie in France?
Dr. Matrix
Thank you, I was worried. Thanks also for the puzzles, makes a change from my usual sudokus. I especially liked 3, 9, 11, 16, 21 and 23.
(anonymous)
@(anonymous): You don't get a confirmation email but if you hit submit you'll be entered. (I'll add confirmation emails before next year...)
Matthew
Do we get a confirmation email after submission of the entry form? I never received one, so I'm not sure if I am entered.
(anonymous)
@Seth: If you find them on the map then that's all you need to do. (And if you didn't find them yet then the entry form won't appear so you definably did everything you need to do.)
Matthew
Add a Comment
2019-09-15
Today, I wrote this LaTeΧ document.
It only uses default LaTeΧ functionality, and uses no packages.
If you compile it (twice so that cross references are not ??s), you will get a four page document (pages numbered i to iv), that repeatedly says:
"This document ends on page v."
If you then recompile it, you will get a five page document (pages numbered i to v), that repeatedly says:
"This document ends on page iv."
Repeatedly compiling it will alternately give these two results, and so the process of compiling this LaTeX document does not converge.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment

















Day 15 - https://oeis.org/A001055 - "number of ways of factoring n with all factors greater than 1"
Day 4 - https://oeis.org/A001045 - "number of ways to tile a 2 × (n-1) rectangle with 1 × 2 dominoes and 2 × 2 squares"
Day 2 - https://oeis.org/A002623 - "number of nondegenerate triangles that can be made from rods of length 1,2,3,4,...,n"